
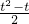 ,n=
,n=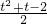 则m(m+k)=
则m(m+k)=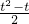 (
(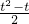 +2t+1)=
+2t+1)= (t4+2t3-t2-2t),n(n+1)=
(t4+2t3-t2-2t),n(n+1)=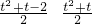 =
= (t4+2t3-t2-2t),因此这样的(m,n)满足条件.综上所述,当k=3时,答案是否定的;当k≥4时,答案是肯定的.
(t4+2t3-t2-2t),因此这样的(m,n)满足条件.综上所述,当k=3时,答案是否定的;当k≥4时,答案是肯定的.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 2 |
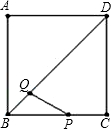 起点运动时,以PQ为直径的⊙O与直线BD的位置关系也随之变化,设运动时间为t(s).
起点运动时,以PQ为直径的⊙O与直线BD的位置关系也随之变化,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | 2 |
 数的函数值y=y3时,对应的x的值为-1<x<0?若存在,求出n的值;若不存在,说明理由.
数的函数值y=y3时,对应的x的值为-1<x<0?若存在,求出n的值;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
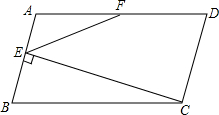 (2012•广州)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(2012•广州)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com