
(9分)已知二次函数![]() 的图象与x轴相交于A、B两点(A
的图象与x轴相交于A、B两点(A
左B右),与y轴相交于点C,顶点为D.
(1)求m的取值范围;
(2)当点A的坐标为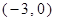 ,求点B的坐标;
,求点B的坐标;
(3)当BC⊥CD时,求m的值.
解:(1)∵二次函数![]() 的图象与x轴相交于A、B两点
的图象与x轴相交于A、B两点
∴b2-4ac>0,∴4+4m>0,······································································· 2分
解得:m>-1························································································· 3分
(2)解法一:
∵二次函数 的图象的对称轴为直线x=-
的图象的对称轴为直线x=-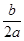 =1························· 4分
=1························· 4分
∴根据抛物线的对称性得点B的坐标为(5,0)··············································· 6分
解法二:
把x=-3,y=0代入 中得m=15··············································· 4分
中得m=15··············································· 4分
∴二次函数的表达式为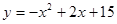
令y=0得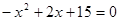 ········································································ 5分
········································································ 5分
解得x1=-3,x2=5
∴点B的坐标为(5,0)··········································································· 6分
(3)如图,过D作DE⊥y轴,垂足为E.
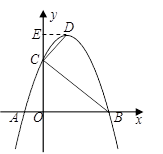
∴∠DEC=∠COB=90°,
当BC⊥CD时,∠DCE +∠BCO=90°,
∵∠DEC=90°,∴∠DCE +∠EDC=90°,∴∠EDC=∠BCO.
∴△DEC∽△COB,∴![]() =
=![]() .····························································· 7分
.····························································· 7分
由题意得:OE=m+1,OC=m,DE=1,∴EC=1.∴ ![]() =
=![]() .
.
∴OB=m,∴B的坐标为(m,0).······························································ 8分
将(m,0)代入![]() 得:-m 2+2 m + m=0.
得:-m 2+2 m + m=0.
解得:m1=0(舍去), m2=3.·································································· 9分
解析:略


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.
已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com