解:(1)∵C点坐标为(4,0),四边形AOCB为正方形,
∴OC=BC=4,
∴B点坐标为(4,4),
又∵E是AB边的中点,
∴E点坐标为(2,4).
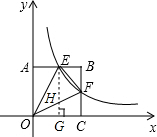
(2)①作EG⊥x轴于G,
∵S
△OEG=S
△OFC,
∴S
△OEG-S
△OHG=S
△OFC-S
△OHG,
∴S
△OH=S
四边形FHEC,
∴S
△OEEF=S
梯形FCGE=

(FC+EG)•GC=

×(2+4)×2=6.
②存在.
∵由(1)可知,E点坐标为(2,4),由(2)知
△OEEF=6,
∴设直线L与x轴的交点为(x,0),则

|x|•FG=6,即

|x|×4=6,解得x=±3,
∴直线L与x轴的交点为(±3,0),
当直线经过点(3,0)时,设直线L的解析式为y=kx+b(k≠0),
∴

,解得
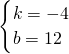
∴此时直线L的解析式为:y=-4x+12;
同理,当当直线经过点(-3,0)时,设直线L的解析式为y=kx+b(k≠0),
∴
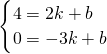
,解得
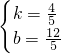
,
∴此时直线L的解析式为:y=

x+

.
故直线L的解析式为:y=-4x+12或y=

x+

.
分析:(1)根据正方形的性质及C点坐标,求出B点坐标,再根据E是AB边的中点,求出E点坐标.
(2)①根据反比例函数k的几何意义,求出S
△OEG=S
△OFC,再根据S
△OEG-S
△OHG=S
△OFC-S
△OHG得知S
△EOH=S
四边形FHEC,再根据S
△EOF=S
梯形FCGE,求出梯形面积即可.
②先设出直线与x轴的交点为x,再根据△OEF的面积列出关于x的方程,求出x的值即可.
点评:本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点、用待定系数法求一次函数的解析式及三角形的面积公式,涉及面较广,难度适中.

 如图,已知点C(4,0)是正方形AOCB的一个顶点,E是AB边的中点.
如图,已知点C(4,0)是正方形AOCB的一个顶点,E是AB边的中点. (x>0)经过点E,且与BC交于点F,连接OE、OF.
(x>0)经过点E,且与BC交于点F,连接OE、OF.
 (FC+EG)•GC=
(FC+EG)•GC= ×(2+4)×2=6.
×(2+4)×2=6. |x|•FG=6,即
|x|•FG=6,即 |x|×4=6,解得x=±3,
|x|×4=6,解得x=±3, ,解得
,解得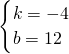
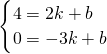 ,解得
,解得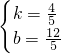 ,
, x+
x+ .
. x+
x+ .
.

 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设