
【题目】现代城市绿化带在不断扩大,绿化用水的节约是一个非常重要的问题.


如图1、图2所示,某喷灌设备由一根高度为0.64 m的水管和一个旋转喷头组成,水管竖直安装在绿化带地面上,旋转喷头安装在水管顶部(水管顶部和旋转喷头口之间的长度、水管在喷灌区域上的占地面积均忽略不计),旋转喷头可以向周围喷出多种抛物线形水柱,从而在绿化带上喷灌出一块圆形区域.现测得喷的最远的水柱在距离水管的水平距离3 m处达到最高,高度为1 m.
(1)求喷灌出的圆形区域的半径;
(2)在边长为16 m的正方形绿化带上固定安装三个该设备,喷灌区域可以完全覆盖该绿化带吗?如果可以,请说明理由;如果不可以,假设水管可以上下调整高度,求水管高度为多少时,喷灌区域恰好可以完全覆盖该绿化带.(以上需要画出示意图,并有必要的计算、推理过程)
【答案】(1)8m;(2)不可以,水管高度调整到0.7m,理由见解析.
【解析】
(1)根据题意设最远的抛物线形水柱的解析式为![]() ,然后将(0,0.64)代入解析式求得a的值,然后求解析式y=0时,x的值,从而求得半径;(2)利用圆与圆的位置关系结合正方形,作出三个等圆覆盖正方形的图形,然后利用勾股定理求得圆的半径,从而使问题得解.
,然后将(0,0.64)代入解析式求得a的值,然后求解析式y=0时,x的值,从而求得半径;(2)利用圆与圆的位置关系结合正方形,作出三个等圆覆盖正方形的图形,然后利用勾股定理求得圆的半径,从而使问题得解.
解:(1)由题意,设最远的抛物线形水柱的解析式为![]() ,将(0,0.64)代入解析式,得
,将(0,0.64)代入解析式,得![]()
解得:![]()
∴最远的抛物线形水柱的解析式为![]()
当y=0时,![]()
解得:![]()
所以喷灌出的圆形区域的半径为8m;
(2)如图,三个等圆覆盖正方形
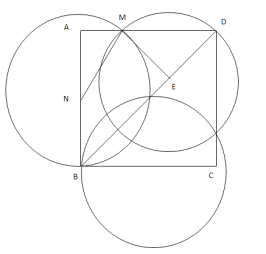
设圆的半径MN=NB=ME=DE=r,则AN=16-r,,MD=![]() ,AM=16-
,AM=16-![]()
∴在Rt△AMN中,![]()
![]()
解得:![]() (其中
(其中![]() ,舍去)
,舍去)
∴![]()
设最远的抛物线形水柱的解析式为![]() ,将(8.5,0)代入
,将(8.5,0)代入
![]()
解得: ![]()
∴![]()
当x=0时,y=![]()
∴水管高度约为0.7m时,喷灌区域恰好可以完全覆盖该绿化带


科目:初中数学 来源: 题型:
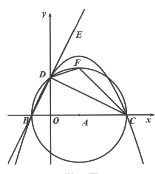
【题目】如图,已知点B的坐标是(-2,0),点C的坐标是(8,0),以线段BC为直径作⊙A,交y轴的正半轴于点D,过B、C、D三点作抛物线.
(1)求抛物线的解析式;
(2)连结BD,CD,点E是BD延长线上一点,∠CDE的角平分线DF交⊙A于点F,连结CF,在直线BE上找一点P,使得△PFC的周长最小,并求出此时点P的坐标;
(3)在(2)的条件下,抛物线上是否存在点G,使得∠GFC=∠DCF,若存在,请直接写出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中国数学名著《九章算术》中,有这样一个问题:“今有共买牛,七家共出一百九十,不足三百三十;九家共出二百七十,盈三十. 问家数、牛价各几何?”大意是:几家人凑钱合伙买牛,如果每7家共出190元,那么还缺少330元钱;如果每9家共出270元,又多了30元钱. 问共有多少人家,每头牛的价钱是多少元?若设有x户人家,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”为我们打开了交流、合作的大门,也为沿线各国在商贸等领域提供了更多的便捷,2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举办,据哈外贸商会发布消息,博览会期间,哈Paseka公司与重庆某国际贸易公司签订了供应蜂蜜合同:哈Paseka公司于2019年6月前分期分批向重庆某国际贸易公司供给优质蜂蜜共3000万件,该公司顺应新时代购物流,打算分线上和线下两种方式销售.
(1)若计划线上销售量不低于线下销售量的25%,求该公司计划在线下销售量最多为多少万件?
(2)该公司在12月上旬销售优质蜂蜜共240万件,且线上线下销售单件均为100元/件.12月中旬决定线上销售单价下调m%,线下销售单价不变,在这种情况下,12月中旬销售总量比上旬增加了m%,且中旬线上销售量占中旬总销量的![]() ,结果中旬销售总金额比上旬销售总金额提高了
,结果中旬销售总金额比上旬销售总金额提高了![]() m%.求m的值.
m%.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
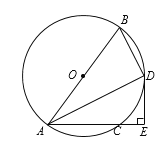
(1)求证:DE是⊙O的切线;
(2)若BD=3,AD=4,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
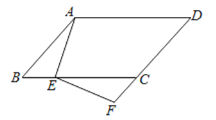
(1) 求证:△ABE∽△ECF;
(2) 若AB=5,AD=8,BE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
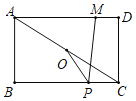
【题目】如图,在矩形ABCD中,AB=3,AD=4,连接AC,O是AC的中点,M是AD上一点,且MD=1,P是BC上一动点,则PM﹣PO的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
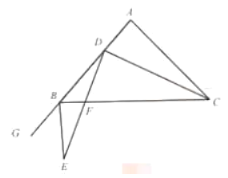
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的动点(点
上的动点(点![]() 不与点
不与点![]() 重合),点
重合),点![]() 在边
在边![]() 的延长线上,
的延长线上,![]() ,
,![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)点![]() 在边
在边![]() 上运动的过程中,
上运动的过程中,![]() 的值是否会发生变化?如果不变化,请求
的值是否会发生变化?如果不变化,请求![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com