
如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与坐标原点重合,顶点
与坐标原点重合,顶点![]() 在坐标轴上,
在坐标轴上,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 轴匀速向点
轴匀速向点![]() 运动,到达点
运动,到达点![]() 即停止.设点
即停止.设点![]() 运动的时间为
运动的时间为![]() .
.![]()
(1)过点![]() 作对角线
作对角线![]() 的垂线,垂足为点
的垂线,垂足为点![]() .求
.求![]() 的长
的长![]() 与时间
与时间![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)在点![]() 运动过程中,当点
运动过程中,当点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好落在对角线
恰好落在对角线![]() 上时,求此时直线
上时,求此时直线![]() 的函数解析式;
的函数解析式;
(3)探索:以![]() 三点为顶点的
三点为顶点的![]() 的面积能否达到矩形
的面积能否达到矩形![]() 面积的
面积的![]() ?请说明理由.
?请说明理由.
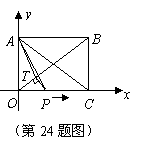
在矩形![]() 中,
中,![]()
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,![]() .
.
![]() ,即
,即![]() ,
,![]() .
.
当点![]() 运动到
运动到![]() 点时即停止运动,此时
点时即停止运动,此时![]() 的最大值为
的最大值为![]() .
.
所以,![]() 的取值范围是
的取值范围是![]() .(2分)
.(2分)
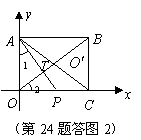 (2)当
(2)当![]() 点关于直线
点关于直线![]() 的对称点
的对称点![]() 恰好在对角线
恰好在对角线![]() 上时,
上时,![]() 三点应在
三点应在![]() 一条直线上(如答图2).
一条直线上(如答图2).
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.![]() 点
点![]() 的坐标为
的坐标为![]() .(1分)
.(1分)
设直线![]() 的函数解析式为
的函数解析式为![]() .将点
.将点![]() 和点
和点![]() 代入解析式,得
代入解析式,得![]() 解这个方程组,得
解这个方程组,得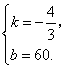
![]() 此时直线
此时直线![]() 的函数解析式是
的函数解析式是![]() .(2)
.(2)
 (3)由(2)知,当
(3)由(2)知,当![]() 时,
时,![]() 三点在一条直线上,此时点
三点在一条直线上,此时点![]() 不构成三角形.(2分)
不构成三角形.(2分)
故分两种情况:
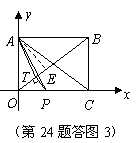
(i)当![]() 时,点
时,点![]() 位于
位于![]() 的内部(如答图3).
的内部(如答图3).
过![]() 点作
点作![]() ,垂足为点
,垂足为点![]() ,由
,由![]()
可得![]() .
.
![]()
![]() .
.
若![]() ,则应有
,则应有![]() ,即
,即![]() .
.
此时,![]() ,所以该方程无实数根.
,所以该方程无实数根.
所以,当![]() 时,以
时,以![]() 为顶点的
为顶点的![]() 的面积不能达到矩形
的面积不能达到矩形![]() 面积的
面积的![]() .(2分)
.(2分)
(ii)当![]() 时,点
时,点![]() 位于
位于![]() 的外部.(如答图4)
的外部.(如答图4)
此时![]() .
.
若![]() ,则应有
,则应有![]() ,即
,即![]() .
.
解这个方程,得![]() ,
,![]() (舍去).
(舍去).
由于![]() ,
,![]() .
.
而此时![]() ,所以
,所以![]() 也不符合题意,故舍去.
也不符合题意,故舍去.
所以,当![]() 时,以
时,以![]() 为顶点的
为顶点的![]() 的面积也不能达到矩形
的面积也不能达到矩形![]() 面积的
面积的![]() .(2分)
.(2分)
综上所述,以![]() 为顶点的
为顶点的![]() 的面积不能达到矩形
的面积不能达到矩形![]() 面积的
面积的![]() .(1分)
.(1分)


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′. | PP′ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 6 |
| x |
| 3 |
| 2 |
| 6 |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:
 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com