Question

如图①在△ABC中，AE=EB，AF=FC，则EF与BC存在以下关系：EF∥BC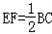，；将AC沿BC方向平移到DH，得图②沿CB方向平移到DH得图③图②中AD与BH存在关系：EF∥AD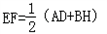，；，那么在图③中是否有类似于图①②中的结论，请把猜想的结论填在方框内，并就图③的结论加以证明．

Answer 1

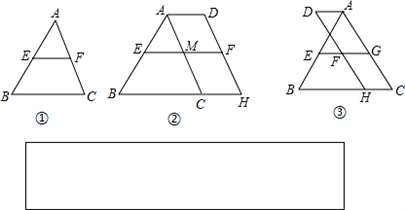解：（1）理由如下：延长EF到点D，使FD=EF， 在△AEF与△CDF中， ， ∵△AEF≌△CDF（SAS）， ∴AE=DC，∠D=∠AEF， ∴CD∥AB， ∵AE=EB， ∴DC=EB， ∴四边形BCDE是平行四边形， ∴ED∥BC，且ED=BC， ∴EF∥BC，且EF=BC； （2）如图②所示，根据（1）得，EG∥BC，且EG=BH， 根据题意得，AD∥BC，CD∥AH， ∴四边形ADCH是平行四边形， ∵EG∥BC， ∴FG=（AD+CH）， ∴EF=EG﹣FG=BH﹣（AD+CH）=（BH﹣CH）﹣AD=（BC﹣AD）； 如图③所示，根据（1）得，EG∥BC，且EG=BH， 根据题意得，AD∥BC，CD∥AH， ∴四边形ADCH是平行四边形， ∵EG∥BC， ∴FG=（AD+CH）， ∴EF=EG+FG=BH+（AD+CH）=（BH+CH）+AD=（BC+AD）．