
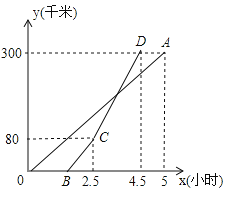
【题目】如图:甲、乙两地相距![]() ,一辆货车和一辆轿车先后从甲地出发驶向乙地,线段
,一辆货车和一辆轿车先后从甲地出发驶向乙地,线段![]() 和折线
和折线![]() 分别表示货车和轿车离甲地的距离
分别表示货车和轿车离甲地的距离![]()
![]() 与货车出发时间
与货车出发时间![]()
![]() 之间的函数关系,请根据图象解答下列问题:
之间的函数关系,请根据图象解答下列问题:
(1)货车的速度为___________![]() ,当轿车到达乙地后,货车距乙地的距离为____________千米;
,当轿车到达乙地后,货车距乙地的距离为____________千米;
(2)求轿车改变速度后![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)轿车到达乙地后,马上沿原路以![]() 段速度返回,求轿车从乙地出发后多长时间再次与货车相遇?
段速度返回,求轿车从乙地出发后多长时间再次与货车相遇?
【答案】(1)60;30;(2)![]() ;(3)
;(3)![]() 小时.
小时.
【解析】
(1)根据函数图象中的数据,可以求得货车的速度和当轿车到达乙地后,货车距乙地的距离;
(2)根据函数图象中的数据可以求得轿车改变速度后y与x的函数关系式;
(3)根据函数图象中的数据可以求得CD段小轿车的速度,从而可以解答本题.
解:(1)由图象可得,
货车的速度为:300÷5=60km/h,
当轿车到达乙地后,货车距乙地的距离为:60×(5-4.5)=30(千米),
故答案为:60,30;
(2)设轿车改变速度后y与x的函数关系式为y=kx+b,![]() ,得
,得![]() ,
,
即轿车改变速度后y与x的函数关系式是y=110x-195(2.5≤x≤4.5);
(3)轿车CD段的速度为:(300-80)÷(4.5-2.5)=110km/h,
设轿车从乙地出发后th时再次与货车相遇,
(110+60)t=300,
解得,t=![]() ,
,
答:轿车从乙地出发后经过![]() 小时再次与货车相遇.
小时再次与货车相遇.


科目:初中数学 来源: 题型:
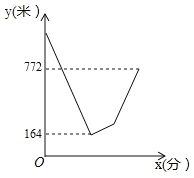
【题目】某个周末小月和小华在南滨路跑步锻炼身体,两人同时从A点出发,沿直线跑到B点后马上掉头原路返回A点算一个来回,回到A点后又马上调头去往B点,以此类推,每人要完成2个来回。一直两人全程均保持匀速,掉头时间忽略不计。如图所示是小华从出发到他率先完成第一个来回为止,两人到B点的距离之和y(米)与小华跑步时间x(分钟)之间的函数图像,则当小华跑完2个来回时,小月离B点的距离为___米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
(1)求证:直线CD是⊙O的切线;
(2)若CM平分∠ACD,且分别交AD,BD于点M,N,当DM=2时,求MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
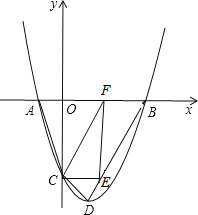
【题目】如图抛物线y=x2+bx+c(c<0)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C,顶点为D,且OB=OC=3,点E为线段BD上的一个动点,EF⊥x轴于F.
(1)求抛物线的解析式;
(2)是否存在点E,使△ECF为直角三角形?若存在,求点E的坐标;不存在,请说明理由;
(3)连接AC、BC,若点P是抛物线上的一个动点,当P运动到什么位置时,∠PCB=∠ACO,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
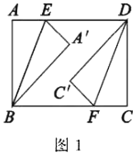
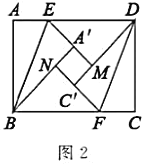
【题目】综合与实践:
动手操作:如图1,四边形![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 边上,且
边上,且![]() ,连接
,连接![]() ,
,![]() .将
.将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折叠,点
折叠,点![]() ,
,![]() 分别落在点
分别落在点![]() ,
,![]() 处.
处.
探究展示:
(1)“刻苦小组”发现:![]() ,且
,且![]() ,并展示了如下的证明过程.
,并展示了如下的证明过程.
证明:在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .(依据1)
.(依据1)
∴![]() .
.
∴![]() .(依据2)
.(依据2)
反思交流:①上述证明过程中的“依据1”与“依据2”分别指什么?
②“勤奋小组”认为:还可以通过证明四边形![]() 是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
猜想证明:
(2)如图2,折叠过程中,当点![]() ,
,![]() 在直线
在直线![]() 的同侧时,延长
的同侧时,延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是什么特殊四边形?请说明理由.
是什么特殊四边形?请说明理由.
联想拓广:
(3)如图3,连接![]() ,
,![]() ,
,![]() .
.

①当![]() 时,
时,![]() 的长为________;
的长为________;
②![]() 的长有最大值吗?若有,请你直接写出
的长有最大值吗?若有,请你直接写出![]() 长的最大值和此时四边形
长的最大值和此时四边形![]() 的形状;若没有,请说明理由.
的形状;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,以下结论:①abc>0;②3a+c>0;③m为任意实数,则有a(m2+1)+bm≥0;④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2,正确的有( )个.
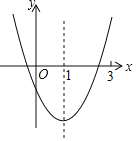
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() :
:![]() 与直线l:
与直线l:![]() 交于x轴上的一点A,和另一点
交于x轴上的一点A,和另一点![]()
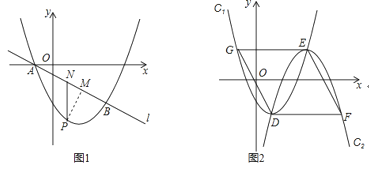
![]() 求抛物线
求抛物线![]() 的解析式;
的解析式;
![]() 点P是抛物线
点P是抛物线![]() 上的一个动点
上的一个动点![]() 点P在A,B两点之间,但不包括A,B两点
点P在A,B两点之间,但不包括A,B两点![]() 于点M,
于点M,![]() 轴交AB于点N,求MN的最大值;
轴交AB于点N,求MN的最大值;
![]() 如图2,将抛物线
如图2,将抛物线![]() 绕顶点旋转
绕顶点旋转![]() 后,再作适当平移得到抛物线
后,再作适当平移得到抛物线![]() ,已知抛物线
,已知抛物线![]() 的顶点E在第一象限的抛物线
的顶点E在第一象限的抛物线![]() 上,且抛持线
上,且抛持线![]() 与抛物线
与抛物线![]() 交于点D,过点D作
交于点D,过点D作![]() 轴交抛物线
轴交抛物线![]() 于点F,过点E作
于点F,过点E作![]() 轴交抛物线
轴交抛物线![]() 于点G,是否存在这样的抛物线
于点G,是否存在这样的抛物线![]() ,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在,请说明理由.
,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校随机抽取部分学生就“你是否喜欢网课”进行问卷调查,并将调查结果进行统计后,绘制成如下统计表和扇形统计图.
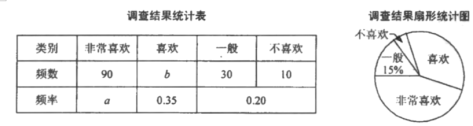
(1)在统计表中,![]() ,
,![]() ;
;
(2)求出扇形统计图中“喜欢”网课所对应扇形的圆心角度数;
(3)己知该校共有2 000名学生,试估计该校“非常喜欢”网课的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
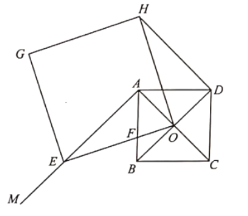
【题目】如图,已知正方形![]() 中,
中,![]() 相交于点
相交于点![]() ,过点
,过点![]() 作射线
作射线![]() ,点
,点![]() 是射线
是射线![]() 上一动点,连接
上一动点,连接![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为一边,作正方形
为一边,作正方形![]() ,且点
,且点![]() 在正方形
在正方形![]() 的内部,连接
的内部,连接![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)连接![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com