
【题目】如图,平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 过
过![]() 点,且与
点,且与![]() 轴交于
轴交于![]() 点.
点.
(1)求点![]() 、点
、点![]() 的坐标;
的坐标;
(2)试说明:![]() ;
;
(3)若点![]() 是直线
是直线![]() 上的一个动点,在
上的一个动点,在![]() 轴上是否存在另一个点
轴上是否存在另一个点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;
;![]() ;(2)见详解;(3)存在,
;(2)见详解;(3)存在,![]() 或
或![]() 或
或![]()
【解析】
(1)令![]() 求出x的值,即可得出点A的坐标;作
求出x的值,即可得出点A的坐标;作![]() ,可知四边形
,可知四边形![]() 是矩形,可得点B的坐标;
是矩形,可得点B的坐标;
(2)先求出点D的坐标,可证![]() ,得出
,得出![]() ,进一步可证明结论;
,进一步可证明结论;
(3)根据平行四边形的对边平行且相等,可得出![]() 再根据点B、M的纵坐标相等,可求得点M的坐标,从而得出BM的值,最后再分情况分析讨论即可得出答案.
再根据点B、M的纵坐标相等,可求得点M的坐标,从而得出BM的值,最后再分情况分析讨论即可得出答案.
解:(1))令![]() ,解得:
,解得:![]() ,点A的坐标为
,点A的坐标为![]() ;
;
作![]() ,四边形
,四边形![]() 是矩形,
是矩形,
∴![]()
∴点B的坐标为![]() ;
;
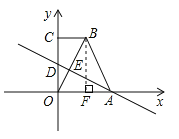
(2)令![]() 中x值为0,解得,
中x值为0,解得,![]() ,点D的坐标为
,点D的坐标为![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
(3)存在点N.理由如下:
∵点N在x轴上,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形
为顶点的四边形是平行四边形
∴![]()
∴点B、M的纵坐标相等
令![]()
解得:![]()
∴![]()
∴![]()
当点N在点O左侧时:点N的坐标为![]() ;
;
当点N在点O右侧时:点N的坐标为![]() ;
;
作点![]() 关于点A对称的点也符合,此时点
关于点A对称的点也符合,此时点![]() 的坐标为
的坐标为![]() .
.
综上所述,点N的坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】完成下列推理论证过程:
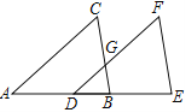
如图,已知∠A=∠EDF,∠C=∠F,
求证:BC∥EF
证明:∵∠A=∠EDF( )
∴________∥________( )
∴∠C=∠BGD( )
又∵∠C=∠F ( 已知 )
∴_______=∠F(等量代换 )
∴BC∥EF( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)如图1,过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,直接写出△PMN为等腰三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:把形如![]() 的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即
的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即![]() .例如:
.例如:![]()
![]() 是
是![]() 的一种形式的配方;所以,
的一种形式的配方;所以,![]() ,
,![]()
![]() ,
,![]() 是
是![]() 的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).
的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).
请根据阅读材料解决下列问题:
(1)比照上面的例子,写出![]() 三种不同形式的配方;
三种不同形式的配方;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人到一家快递公司办理环江香米(简称香米)的快递托运,重量为![]() 千克.快递公司收取托运费方案如下:
千克.快递公司收取托运费方案如下:
凡物品重量不超过10千克的,按2元/千克收取托运费;当物品重量超过10千克的,超出部分按3元/千克加收托运费.
(1)写出![]() 千克香米的托运费的表达式 (用含字母
千克香米的托运费的表达式 (用含字母![]() 的式子表示);
的式子表示);
(2)若托运香米重量为![]() 千克时,求出这笔托运费.
千克时,求出这笔托运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣3,3 ![]() ),反比例函数y=
),反比例函数y= ![]() 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是 .
的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com