
【题目】已知![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 由
由![]() 出发沿
出发沿![]() 向点
向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由
由![]() 出发沿
出发沿![]() 向点
向点![]() 匀速运动,它们的速度相同,点
匀速运动,它们的速度相同,点![]() 在
在![]() 上,
上,![]() ,且点
,且点![]() 在点
在点![]() 的下方,当点
的下方,当点![]() 到达点
到达点![]() 时,点
时,点![]() ,
,![]() 也停止运动,连接
也停止运动,连接![]() ,设
,设![]() .解答下列问题:
.解答下列问题:
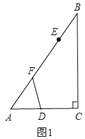
![]() 如图
如图![]() ,当
,当![]() 为何值时,
为何值时,![]() 为直角三角形;
为直角三角形;
![]() 如图
如图![]() ,把
,把![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 点.
点.
①当![]() 为何值时,四边形
为何值时,四边形![]() 为菱形?并求出菱形的面积;
为菱形?并求出菱形的面积;
②如图![]() ,分别取
,分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,在整个运动过程中,则线段
,在整个运动过程中,则线段![]() 扫过的区域的形状为________,其面积为________.
扫过的区域的形状为________,其面积为________.


【答案】平行四边形![]()
【解析】
(1)△ADF为直角三角形,有两种可能:∠ADF=90°或∠AFD=90°,根据锐角三角函数,分两种情况进行讨论,列方程求解即可;
(2)①根据菱形的判定,可知当AD=DF时,四边形ADFD′为菱形,根据锐角三角函数列方程求出x,计算菱形的面积即可;②根据三角形中位线定理可知,线段MN扫过的区域的形状是平行四边形,其面积为![]() .
.
解:(1)∵∠ACB=90°,BC=8,tanA=![]()
∴BC=8,AB=10,
∴AD=x,BE=x,AF=6-x,
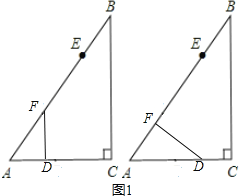
当∠ADF=90°,如图1左图,
∵tanA=![]()
∴cosA=![]()
∴![]()
x=![]() ;
;
当∠AFD=90°,如图1右图,
∵tanA=![]()
∴cosA=![]()
∴![]()
x=![]() ,
,
∴当
x=![]() 或x=
或x=![]() ,
,
△ADF为直角三角形;
(2)①如图2,
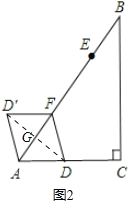
∵AD=AD′,D′F=DF,
∴当AD=DF时,四边形ADFD′为菱形,
∴连接DD′⊥AF于G,AG=![]() ,
,
∵tanA=![]() ,
,
∴cosA=![]() ,
,
∴![]() ,
,
∴x=![]() ,
,
S菱形=![]() ×DD′×AF=
×DD′×AF=![]() ×
×![]() ×
×![]() =
=![]() ;
;
②平行四边形,![]()
∵M、N分别为D′F、D′E的中点,
∴MN∥EF,MN=![]() EF=2,
EF=2,
∴线段MN扫过的区域的形状是平行四边形,
当D运动到C,则F正好运动到A,此时MA=![]() D′A=
D′A=![]() DA=3,
DA=3,
∵∠DAB=∠D′AB,
∴tanA=tan∠D′AB=![]() ,
,
点M到AB的距离设为4x,则(3x)2+(4x)2=32,
解得:x=![]() ,
,
4x=![]()
∴线段MN扫过的区域的形状是平行四边形的面积=2×![]() =
=![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
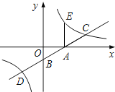
【题目】如图,直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与反比例函数
,与反比例函数![]() 图象交于点
图象交于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线交该反比例函数图象于点
轴的垂线交该反比例函数图象于点![]() .
.
![]() 求点
求点![]() 的坐标.
的坐标.
![]() 若
若![]() .
.
①求![]() 的值.
的值.
②试判断点![]() 与点
与点![]() 是否关于原点
是否关于原点![]() 成中心对称?并说明理由.
成中心对称?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(-2,1),B(-3,4),C(-1,3),过点(l,0)作x轴的垂线![]() .
.
(1)作出△ABC关于直线![]() 的轴对称图形△
的轴对称图形△![]() ;
;
(2)直接写出A1(___,___),B1(___,___),C1(___,___);
(3)在△ABC内有一点P(m,n),则点P关于直线![]() 的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).
的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线![]() 相交于A(1,
相交于A(1,![]() ),B(4,0)两点.
),B(4,0)两点.

(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 为菱形,点
为菱形,点![]() 为对角线
为对角线![]() 上的一个动点,连接
上的一个动点,连接![]() 并延长交射线
并延长交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 是否存在这样一个菱形,当
是否存在这样一个菱形,当![]() 时,刚好
时,刚好![]() ?若存在,求出
?若存在,求出![]() 的度数;若不存在,请说明理由;
的度数;若不存在,请说明理由;
![]() 若
若![]() ,且当
,且当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中华人民共和国道路交通管理条例》规定:小汽车在城街路上行驶速度不得超过70 km/h,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪 A的正前方60 m处的C点,过了5 s后,测得小汽车所在的B点与车速检测仪A之间的距离为100 m.
(1)求B,C间的距离.
(2)这辆小汽车超速了吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种折叠式可调节的鱼竿支架的示意图,AE是地插,用来将支架固定在地面上,支架AB可绕A点前后转动,用来调节AB与地面的夹角,支架CD可绕AB上定点C前后转动,用来调节CD与AB的夹角,支架CD带有伸缩调节长度的伸缩功能,已知BC=60cm.
(1)若支架AB与地面的夹角∠BAF=35°,支架CD与钓鱼竿DB垂直,钓鱼竿DB与地面AF平行,则支架CD的长度为 cm(精确到0.1cm);(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70).
(2)如图2,保持(1)中支架AB与地面的夹角不变,调节支架CD与AB的夹角,使得∠DCB=85°,若要使钓鱼竿DB与地面AF仍然保持平行,则支架CD的长度应该调节为多少?(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com