
【题目】某公司生产一种节能型灯具并加以销售,现准备在甲市和乙市按不同的方案进行销售,若只在甲市销售,销售价为![]() (元/件),月销售量为
(元/件),月销售量为![]() (件),
(件),![]() 是
是![]() 的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为
的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为![]() (元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为
(元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为![]() 元/件(
元/件(![]() 为常数且
为常数且![]() ),当月销售量为
),当月销售量为![]() 件时,每月还需交纳
件时,每月还需交纳![]() 的附加费,设月利润为
的附加费,设月利润为![]() (元).(利润=销售额-成本-附加费)
(元).(利润=销售额-成本-附加费)
月销售量 | 1500 | 2000 |
销售价格 | 185 | 180 |
(1)当![]() 时,
时,![]() ______元/件,
______元/件,![]() ______元(直接写出结果).
______元(直接写出结果).
(2)分别求出![]() 、
、![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的取值范围).
的取值范围).
(3)当![]() 为何值时,
为何值时,![]() 最大?若在乙市销售月利润最大值与甲市最大值相同,求
最大?若在乙市销售月利润最大值与甲市最大值相同,求![]() 的值.
的值.
【答案】(1)190,67500;(2)![]() ,
,![]() ;(3)7500,60.
;(3)7500,60.
【解析】
(1)设![]() ,把x=1500,y=185;x=2000,y=180,代入
,把x=1500,y=185;x=2000,y=180,代入![]() ,得到关于k,b的二元一次方程组,求出k,b的值即可,再根据
,得到关于k,b的二元一次方程组,求出k,b的值即可,再根据![]() ,求出
,求出![]() 的解析式,分别求出当x=1000时,
的解析式,分别求出当x=1000时,![]() ,
,![]() 的值即可;
的值即可;
(2)根据“利润=销售额-成本-广告费”和“利润=销售额-成本-附加费”,分别求出![]() 、
、![]() 与
与![]() 的函数关系式即可;
的函数关系式即可;
(3)根据二次函数图象的顶点坐标公式,即可求得![]() 最大时,所对应的x的值,然后根据题意列出关于a的方程,即可求解.
最大时,所对应的x的值,然后根据题意列出关于a的方程,即可求解.
(1)设![]() ,
,
由题意得:![]() ,解得
,解得 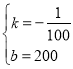 ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() ,
,
∵ ![]()
∴当![]() 时,
时,![]() ,
,
故答案是:190,67500;
(2)由题意得:![]() ,
,
![]() .
.
(3)∵![]()
∴当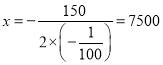 时,
时,![]() 最大.
最大.
由题意得: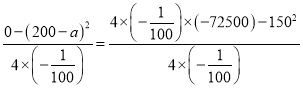 ,解得
,解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣3)2+![]() 过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切.正确的结论是( )
过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切.正确的结论是( )
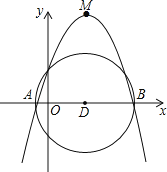
A.①③B.①④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
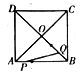
【题目】如图,四边形ABCD是正方形,![]() ,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是
,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是![]() ,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,
,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,![]() 的面积为y,则y关于x的函数图象大致为( )
的面积为y,则y关于x的函数图象大致为( )
A.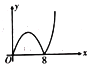 B.
B.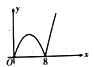 C.
C. D.
D.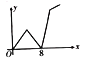
查看答案和解析>>
科目:初中数学 来源: 题型:
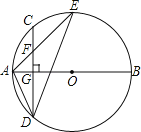
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=![]() ;④S△DEF=4
;④S△DEF=4![]() .
.
其中正确的是 (写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
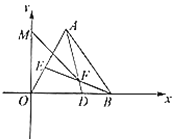
【题目】如图,在平面直角坐标系中,等边![]() 的边
的边![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() ,
,![]() ,点
,点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 出发以相同的速度向
出发以相同的速度向![]() 、
、![]() 运动,连接
运动,连接![]() 、
、![]() 交于点
交于点![]() ,
,![]() 是
是![]() 轴上一点,则
轴上一点,则![]() 的最小值为______.
的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,将边BC折叠,使点B落在OA上的点D处,已知折痕CE=5![]() ,且4AE=3AD.
,且4AE=3AD.
①判断△OCD与△ADE是否相似,请说明理由。
②求直线CE与x轴的交点P的坐标。
③是否存在过点D的直线l,使直线l与两坐标轴围成的三角形与直线CE与两坐标轴围成的三角形相似,如果存在,请求出其解析式,如果不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() (
(![]() )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;
②3a+b<0;
③![]() ;
;
④![]() ;
;
其中正确的结论是( )

A.①③④B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,

(1)图1中共有_______对相似三角形;
(2)已知![]() ,请求出
,请求出![]() 的长;
的长;
(3)在(2)的情况下,如果以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,点
轴,点![]() 为坐标原点
为坐标原点![]() ,建立直角坐标系(如图2),若点
,建立直角坐标系(如图2),若点![]() 从
从![]() 点出发,以每秒1个单位的速度沿线段
点出发,以每秒1个单位的速度沿线段![]() 运动,点
运动,点![]() 出
出![]() 点出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动:设运动时间为
点出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动:设运动时间为![]() 秒是否存在点
秒是否存在点![]() ,使以点
,使以点![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
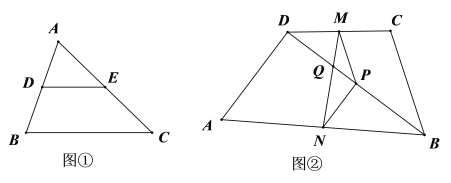
【题目】教材呈现:下图是华师版九年级上册数学教材第77页的部分内容.
猜想:

如图,在![]() 中,点
中,点![]() 分别是
分别是![]() 与
与![]() 的中点,根据画出的图形,可以猜想:
的中点,根据画出的图形,可以猜想:
![]() ,且
,且![]() .
.
对此,我们可以用演绎推理给出证明.
证明:在![]() 中,
中,
∵点![]() 分别是
分别是![]() 与
与![]() 的中点,
的中点,
∴![]() .
.
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:
如图②在四边形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() _______________.
_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com