
����Ŀ���Ķ�������ϣ��ش�����
�����ܹ���������
�ƴ�������ѧ�Һ�������ʫ�������С�������֣���ɫң����ȴ�ޣ�
����ӡ������ʫ��̩����ڡ���������ңԶ�ľ��롷��д����
����������ңԶ�ľ���
����˲�����Ѱ��
���������
��ע���������
��������ѧ������ѧ������ѧ�е����Ż��⣬Ψ�ж����������в��������������������߶ȣ�
��֪�� A��B �������Ϸֱ��ʾ������ a��b��A��B ����֮��ľ����ʾΪ AB��
��![]() ���� A��B ��������һ����ԭ��ʱ��������� A ��ԭ�㣬��ͼ 1��
���� A��B ��������һ����ԭ��ʱ��������� A ��ԭ�㣬��ͼ 1��![]() ��
��
��![]() ���� A��B ���㶼����ԭ��ʱ��
���� A��B ���㶼����ԭ��ʱ��
����ͼ 2���� A��B ����ԭ����ұߣ�![]() ��
��
����ͼ 3���� A��B ����ԭ�����ߣ�![]() ��
��
����ͼ 4���� A��B ��ԭ������ߣ�![]() ��
��
���ϣ������� A��B ����ľ��� ![]() ��
��
�����������ۣ��ش������������⣺
![]()
��1���������ϱ�ʾ ![]() ��
��![]() ������֮��ľ�����
������֮��ľ�����![]() ����
���� ![]() ��
��
��2��������ʽ ![]() ȡ��Сֵʱ����
ȡ��Сֵʱ����![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
��3����δ֪�� ![]() ��
��![]() ����
���� ![]() �������ʽ
�������ʽ ![]() �����ֵ�� ����Сֵ�� ��
�����ֵ�� ����Сֵ�� ��
���𰸡���1��-6��2����2��-1��x��2����3��7��-1��
��������
��1��������ת��Ϊ����ֵ���̣����ɽ�����⣮
��2��������ʽ|x+1|+|x-2|ȡ��Сֵʱ����ʾ����������һ��x����-1��2�ľ���֮����С����Ȼ�����x��-1��2֮�䣨����-1��2�����ɴ˼��ɽ�����⣮
��3������Ϊ��|x-1|+|x-3|����|y-2|+|y+1|��=6������Ϊ|x-1|+|x-3|����СֵΪ2��|y-2|+|y+1|����СֵΪ3������1��x��3��-1��y��2���ɴ˲��ѵõ��𰸣�
��1���������ϱ�ʾx��-2������֮��ľ�����4��
��|x+2|=4��
���x=-2-4=-6��x=-2+4=2��
�ʴ�Ϊ-6��2��
��2��������ʽ|x+1|+|x-2|ȡ��Сֵʱ����ʾ����������һ��x����-1��2�ľ���֮����С����Ȼ�����x��-1��2֮�䣨����-1��2����
��x��ȡֵ��Χ��-1��x��2��
�ʴ�Ϊ-1��x��2��
��3���ߣ�|x-1|+|x-3|����|y-2|+|y+1|��=6��
�֡�|x-1|+|x-3|����СֵΪ2��|y-2|+|y+1|����СֵΪ3��
��1��x��3��-1��y��2��
�����ʽx+2y�����ֵ��7����Сֵ��-1��
�ʴ�Ϊ7��-1��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��һ��ֱ���ϣ�![]() ��
��![]() ��Ϊ�ȱ������Σ�����AE��CD.AE�ֱ�CD��BD�ڵ�M��P.CD��BE�ڵ�Q��
��Ϊ�ȱ������Σ�����AE��CD.AE�ֱ�CD��BD�ڵ�M��P.CD��BE�ڵ�Q��
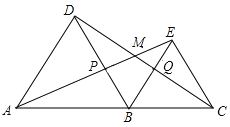
��֤����1��![]() ��
��
��2������MB��MBƽ��![]() �𣿲�˵�����ɣ�
�𣿲�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ��DZ�BC��AB�ϵĵ㣬��CE=BF������DE������E��EG��DE��ʹEG=DE������FG��FC��
��1�����жϣ�FG��CE�Ĺ�ϵ��___��
��2����ͼ2������E��F�ֱ��DZ�CB��BA�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ�������������жϲ�����֤����
��3����ͼ3������E��F�ֱ��DZ�BC��AB�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ��������ֱ��д������жϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����в��ŶԱ��������꼶��ѧ��������һ����������ʾ����飬����������һ�����⣺��ʦ�ڿ����Ϸ�����ѧ�����ʺͱ�� ��
A���Ӳ� B������ C����ʱ D������ E������
�����ѧ���������ѡ����ֻ��ѡ��һ������Ǹ���ѧ���Ը�����Ĵ��������Ƶ�������������ͳ��ͼ��
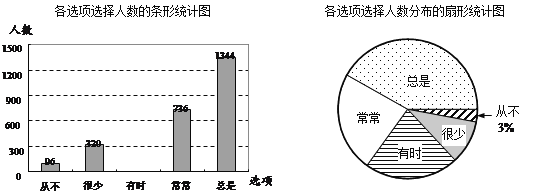
����������Ϣ������������⣺
��1���������� �������꼶��ѧ���μ��˱����ʾ����飻
��2������������ͳ��ͼ����������
��3��������ͳ��ͼ�У������ǡ���Բ�Ľ�Ϊ ������ȷ���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺![]() �ǹ���
�ǹ��� ![]() ��
��![]() �Ķ���ʽ�����
�Ķ���ʽ����� ![]() ����ô
����ô ![]() �������Գƶ���ʽ�������磬���
�������Գƶ���ʽ�������磬��� ![]() ,��
,�� ![]() ��Ȼ ������
��Ȼ ������ ![]() �����Գƶ���ʽ����
�����Գƶ���ʽ����
��1��![]() �����Գƶ���ʽ������˵�����ɣ�
�����Գƶ���ʽ������˵�����ɣ�
��2����дһ�����Գƶ���ʽ����![]() �������������
�������������
��3����� ![]() ��
�� ![]() ��Ϊ���Գƶ���ʽ������ô
��Ϊ���Գƶ���ʽ������ô ![]() һ�������Գƶ���ʽ����?���һ������˵�����ɣ������һ���������˵����
һ�������Գƶ���ʽ����?���һ������˵�����ɣ������һ���������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��CD����A=��C=100�㣬E��F��CD�ϣ��������DBF=��ABD��BEƽ�֡�CBF��
��1��ֱ��AD��BC�к�λ�ù�ϵ����˵������.
��2�����DBE�Ķ�����
��3������AD����ƽ���ƶ�����ƽ���ƶ�AD�Ĺ����У��Ƿ����ij�������ʹ��BEC=��ADB�������ڣ������ʱ��ADB�Ķ������������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��C��D�ĸ���վ��λ����ͼ��ʾ��A��B��վ֮��ľ���AB��a��b��B��C��վ֮��ľ���BC��2a��b��B��D��վ֮��ľ���BD��![]() ��
��
(1)��A��C��վ֮��ľ���AC.
(2)��A��C��վ֮��ľ���AC��90km����C��D��վ֮��ľ���CD��
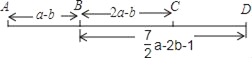
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�ֶ�������n����F�����㣺�ٵ�nΪ����ʱ��F��n��=3n+1���ڵ�nΪż��ʱ��F��n��=![]() ������k��ʹF��n��Ϊ���������������������������㽻���ظ����У����磬ȡn=24����
������k��ʹF��n��Ϊ���������������������������㽻���ظ����У����磬ȡn=24����
![]()
��n=13�����2018����F������Ľ���ǣ�������
A. 1 B. 4 C. 2018 D. 42018
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ϊ1����Ϊa�ľ���ֽƬ��![]() ������ͼ������һ�£�����һ���߳����ھ��ο��ȵ������Σ���Ϊ��һ�β��������ٰ�ʣ�µľ�����ͼ������һ�£�����һ���߳����ڴ�ʱ���ο��ȵ������Σ���Ϊ�ڶ��β���������˷���������ȥ�����ڵ�n�˲�����ʣ�µľ���Ϊ�����Σ��������ֹ����n=3ʱ��a��ֵΪ�� ��
������ͼ������һ�£�����һ���߳����ھ��ο��ȵ������Σ���Ϊ��һ�β��������ٰ�ʣ�µľ�����ͼ������һ�£�����һ���߳����ڴ�ʱ���ο��ȵ������Σ���Ϊ�ڶ��β���������˷���������ȥ�����ڵ�n�˲�����ʣ�µľ���Ϊ�����Σ��������ֹ����n=3ʱ��a��ֵΪ�� ��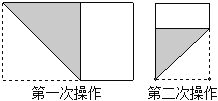
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com