已知直角三角形ABC和ADC有公共斜边AC,M、N分别是AC,BD中点,且M、N不重合.
(1)线段MN与BD是否垂直?请说明理由;
(2)若∠BAC=30°,∠CAD=45°,AC=4,求MN的长.
【答案】
分析:(1)根据题意画出图形,再作出辅助线构成等腰三角形,利用等腰三角形的性质进行证明;
(2)注意要分二种情况讨论:即B、D在AC两侧和B、D在AC同侧.
解答:解:(1)线段MN与BD垂直.
连接MB与MD,由直角三角形斜边上的中线等于斜边长的一半,可以知道
MB=

,MD=
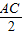
,所以MB=MD.
三角形MBD中,N是底边上的中点,等腰三角形的性质可以说明:
MN垂直BD.
(2)如图一:连接BM、MD,延长DM,过B作DM延长线的垂线段BE,
则可知在Rt△BEM中,∠EMB=30°,
∵AC=4,∴BM=2,
∴BE=1,EM=
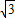
,MD=2,
从而可知
BD=

=2
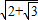
∴BN=

.

由Rt△BMN可得:
MN=
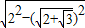
=
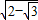
.
如图二:连接BM、MD,延长AD,过B作垂线段BE,
∵M、N分别是AC,BD中点,
∴MD=

AC,MB

AC,
∴MD=MB,
∵∠BAC=30°,∠CAD=45°,
∴∠BMC=60°,∠DMC=90°,
∴∠BMD=30°,
∴∠BDM=
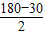
=75°,
∵∠MDA=45°
∴∠EDB=180°-∠BDM-∠MDA=60°,
令ED=x,则BE=
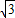
x,AD=2
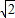
,AB=2
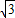
,
∴由Rt△ABE可得:(2
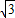
)
2=(
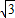
x)
2+(x+2
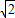
)
2,
解得x=
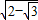
,则BD=2
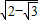
,
∵M、N分别是AC,BD中点,
∴MD=2 DN=
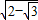
.
由Rt△MND可得:
MN=

=
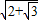
.
点评:本题综合考查了等腰三角形的性质和解直角三角形的方法,同时考查了分类讨论思想.

 ,MD=
,MD=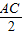 ,所以MB=MD.
,所以MB=MD.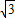 ,MD=2,
,MD=2, =2
=2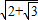
 .
.
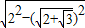 =
=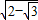 .
. AC,MB
AC,MB AC,
AC,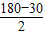 =75°,
=75°,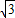 x,AD=2
x,AD=2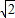 ,AB=2
,AB=2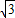 ,
,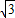 )2=(
)2=(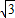 x)2+(x+2
x)2+(x+2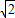 )2,
)2,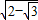 ,则BD=2
,则BD=2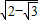 ,
,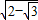 .
. =
=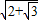 .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 21、根据下列语句作图、测量和比较.
21、根据下列语句作图、测量和比较.