
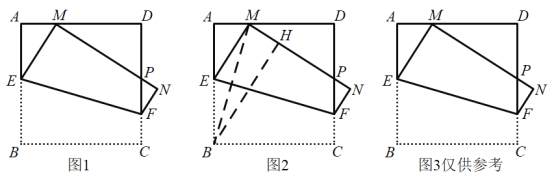
����Ŀ����ͼ1���ڱ߳�Ϊ1��������ABCD�У�����E��F�ֱ��ڱ�AB��CD�ϣ���������ABCD��ֱ��EF�۵���ʹ��B�Ķ�Ӧ��Mʼ�����ڱ�AD��(��M�����A��D�غ�)����C���ڵ�N����MN��CD���ڵ�P����BE��x��
(1)��AM��![]() ʱ����x��ֵ��
ʱ����x��ֵ��
(2)��ͼ2������BM����B����BH��MN������ΪH����֤��BM����ABH�Ľ�ƽ���ߣ�
(3)���ŵ�M�ڱ�AD��λ�õı仯����PDM���ܳ��Ƿ����仯����仯����˵�����ɣ��粻�䣬������ö�ֵ��
(4)���ı���BEFC�����ΪS����S��x֮��ĺ�������ʽ�������S����Сֵ��
���𰸡���1��x��![]() ����2��֤������������3�����䣬��DMP���ܳ�Ϊ2����4��S��
����2��֤������������3�����䣬��DMP���ܳ�Ϊ2����4��S��![]() (2x��
(2x��![]() )���������СֵΪ
)���������СֵΪ![]() ��
��
��������
��1�����ù��ɶ����������̣����ɽ�����⣻
��2��ͨ��֤����BAM�ա�BHM�����ɵ���ABM����MBH�����ɵ�֤��
��3����AM��y����BE��EM��x��MD��1��y����Rt��AEM�У��ɹ��ɶ����ó�x��y�Ĺ�ϵʽ����֤Rt��AEM��Rt��DMP���������������ε��ܳ��ȵ������Ʊ����DMP���ܳ���
��4����FH��AB��H�����ı���BCFH�Ǿ��Σ�����BM��EF��O����FH��K���������ε������ʽ�������κ��������ö��κ��������ʽ����ֵ���⼴�ɣ�
�⣺��1����ͼ����Rt��AEM�У�AE��1��x��EM��BE��x��AM��![]() ��
��
��AE2+AM2��EM2��
�ࣨ1��x��2+��![]() ��2��x2��
��2��x2��
��x��![]() ��
��
��2����EB��EM��
���EBM����EMB��
�ߡ�EBC����EMN��
���MBC����BMN��
��AD��BC��
����MBC����AMB��
����AMB����BMN��
���ߡ�A����MHB��BM��BM��
���BAM�ա�BHM��
���ABM����MBH��
��BM����ABH�Ľ�ƽ���ߣ�
��3����DMP���ܳ����䣬Ϊ2��
���ɣ���AM��y����BE��EM��x��MD��1��y��
��Rt��AEM�У��ɹ��ɶ�����AE2+AM2��EM2��
�ࣨ1��x��2+y2��x2��
���1+y2��2x��
��1��y2��2��1��x��
�ߡ�EMP��90�㣬��A����D��
��Rt��AEM��Rt��DMP��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
���DM![]() ��2��
��2��
���DMP���ܳ����䣬Ϊ2��
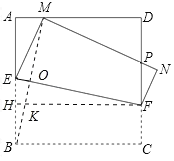
��4����FH��AB��H������BM��EF��O����FH��K��
���ı���BCFH�Ǿ��Σ�
��Rt��AEM��AM��![]() ��
��![]() ��
��
��B��M����EF�Գƣ�
��BM��EF��
���KOF����KHB��
�ߡ�OKF����BKH��
���KFO����KBH��
��AB��BC��FH����A����FHE��90�㣬
���ABM�ա�HFE��
��EH��AM��![]() ��
��
��CF��BH��x��![]() ��
��
��S��![]() ��BE+CF��BC
��BE+CF��BC
��![]() ��x+x��
��x+x��![]() ��
��
��![]() ��2x��
��2x��![]() ��
��
��![]() [��
[��![]() ��2��
��2��![]() +1]
+1]
��![]() ��
��![]() ��
��![]() ��2+
��2+![]() ��
��
��S��![]() ��2x��
��2x��![]() ����
����
��![]() ��
��![]() ʱ��S����Сֵ��
ʱ��S����Сֵ��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ž���ֽ���Բ��ֽ�尴��ͼ��ʽ�ֱ����ͬ����������ͼ��AC=3��BC=4��AB=5���ֱ������߳������������) ��ͼ1�б�HI��LM�͵�K��J��ǡ���ھ���ֽ��ı��ϣ�ͼ2�е�Բ��O��AB�е㴦����H��I����Բ�ϣ�����κ�Բ��ֽ���������ǣ� ��
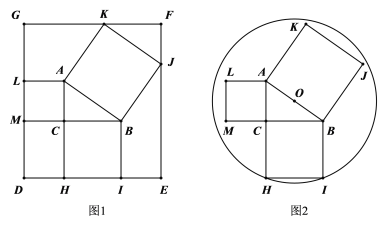
A.400:127��B.484:145��C.440:137��D.88:25��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
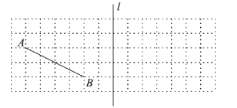
����Ŀ����ͼ����![]() �������У�ÿ��С�����εı߳���Ϊ
�������У�ÿ��С�����εı߳���Ϊ![]() �������ߵĽ����Ϊ��㣬�Ը��Ϊ����������γ�Ϊ��������Σ���ֱ֪��
�������ߵĽ����Ϊ��㣬�Ը��Ϊ����������γ�Ϊ��������Σ���ֱ֪��![]() �����
�����![]() ��
��![]() ������
������![]() ��
��
��1�����������Ҫ�����λ�ͼ��
����ֱ��![]() �������һ�����
�������һ�����![]() ����
����![]() ����ֱ��
����ֱ��![]() �ϣ�����������
�ϣ�����������![]() ��ֱ�������Σ�
��ֱ�������Σ�
�ڻ���![]() ����ֱ��
����ֱ��![]() ����Գ�
����Գ�![]() ��
��
��2�����㣨1����![]() ��������ֵΪ���٣�
��������ֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
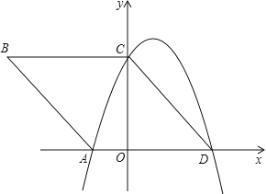
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У��ı���ABCD�DZ߳�Ϊ5�����Σ�����A��C��D�����������ϣ�sinB=![]() ��
��
��1�����A��C��D����������ߵĽ���ʽ��
��2����ֱ��AB�Ľ���ʽΪy1=mx+n����1���������ߵĽ���ʽΪy2=ax2+bx+c����y1>y2ʱ���Ա���x��ȡֵ��Χ��
��3����ֱ��AB�루1���������ߵ���һ������ΪE��P��Ϊ��������A��E����֮���һ�����㣬��ֱ��PE��x���ڵ�F���ʣ���P���ںδ�ʱ����PAE�������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ֱ�DZ߱�Ϊ1��2��ֱ�������ν����ͺ������Σ�
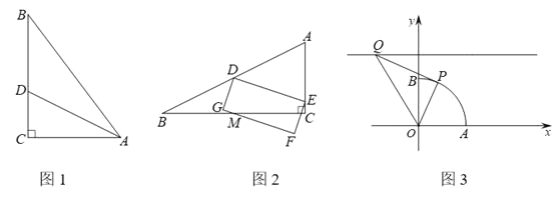
��1����ͼ1����ABC�У���C= ![]() ��AC=3��BC=4��ADƽ�֡�CAB��BC�ڵ�D��˵����ACD�Ǻͺ������Σ�
��AC=3��BC=4��ADƽ�֡�CAB��BC�ڵ�D��˵����ACD�Ǻͺ������Σ�
��2����ͼ2���ͺ���ABC�У���C= ![]() ��AC=
��AC= ![]() ����D�DZ�AB�е㣬��E�DZ�AC��һ���㣬��ֱ��DE�·��������DEFG��ʹֱ��FGʼ�վ���BC�е�M����֪��ABC���Ϊ4�������DEFG�������
����D�DZ�AB�е㣬��E�DZ�AC��һ���㣬��ֱ��DE�·��������DEFG��ʹֱ��FGʼ�վ���BC�е�M����֪��ABC���Ϊ4�������DEFG�������
��3����ͼ3������OAB�У���AOB= ![]() ��OA=2���Ե�OΪԭ�㣬OA��OB����ֱ��Ϊ�����Ὠ��ƽ��ֱ������ϵ����P��
��OA=2���Ե�OΪԭ�㣬OA��OB����ֱ��Ϊ�����Ὠ��ƽ��ֱ������ϵ����P�� ![]() һ���㣬��Q��ֱ��y=3��һ���㣬����OPQ�Ǻͺ�������ʱ�����P���꣮
һ���㣬��Q��ֱ��y=3��һ���㣬����OPQ�Ǻͺ�������ʱ�����P���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
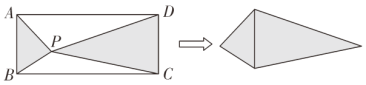
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ��P�Ǿ���
��P�Ǿ���![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ��
��![]() ��
��![]() ��������μ�����Ȼ���������Ӱ������ƴ��һ���ı��Σ�������ı��ε����Ϊ_________������ı����ܳ�����СֵΪ________.
��������μ�����Ȼ���������Ӱ������ƴ��һ���ı��Σ�������ı��ε����Ϊ_________������ı����ܳ�����СֵΪ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲���������������A��B����֮��ľ��룬����ʵ�������������ͼͼ�Σ�����AB��BE��EF��BE��AF��BE��D��C��BD�ϣ�����λͬѧ�ֱ�����������������ݣ���BC����ACB�� ��CD����ACB����ADB����EF��DE��BD����DE��DC��BC���ܸ����������ݣ����A��B���������� ��

A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�о���ѧϰС�����ѧУ���AB�ĸ߶ȣ���ͼ�ڽ�ѧ¥һ¥C�������˶���������Ϊ60�����ڽ�ѧ¥��¥D�������˶���������Ϊ30������˵ײ����ѧ¥һ¥��ͬһˮƽ���ϣ���֪ÿ��¥�ĸ߶�Ϊ3�ף������AB�ĸ߶�Ϊ
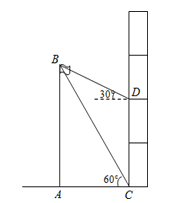
A.9��B.6![]() ��C.6��D.��6+
��C.6��D.��6+![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�E��F�ֱ���DA��BC�ӳ����ϵĵ㣬�ҡ�ABE����CDF��
��֤����1����ABE�ա�CDF��
��2���ı���EBFD��ƽ���ı��Σ�
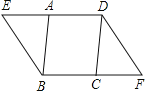
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com