
阅读下列材料:
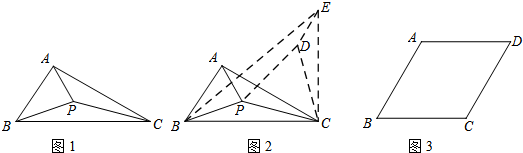
小华遇到这样一个问题,如图1,△ABC中,∠ACB=30º,BC=6,AC=5,在△ABC内部有一点P,连接PA.PB.PC,求PA+PB+PC的最小值.

小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折.旋转.平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60º,得到△EDC,连接PD.BE,则BE的长即为所求.
(1)请你写出图2中,PA+PB+PC的最小值为 ;
(2)参考小华的思考问题的方法,解决下列问题:
①如图3,菱形ABCD中,∠ABC=60º,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);
②若①中菱形ABCD的边长为4,请直接写出当PA+PB+PC值最小时PB的长.
(1)PA+PB+PC的最小值为 ;
;
(2)①图形见解析;②当PA+PB+PC值最小时PB的长为 .
.
【解析】
试题分析:(1)先由旋转的性质得出△APC≌△EDC,则∠ACP=∠ECD,AC=EC=5,∠PCD=60°,再证明∠BCE=90°,然后在Rt△BCE中,由勾股定理求出BE的长度,即为PA+PB+PC的最小值;
(2)①将△APC绕点C顺时针旋转60°,得到△DEC,连接PE.DE,则线段BD即为PA+PB+PC最小值的线段;
②当B.P.E.D四点共线时,PA+PB+PC值最小,最小值为BD.先由旋转的性质得出△APC≌△DEC,则CP=CE,再证明△PCE是等边三角形,得到PE=CE=CP,然后根据菱形.三角形外角的性质,等腰三角形的判定得出BP=CP,同理,得出DE=CE,则BP=PE=ED= BD.
BD.
试题解析:(1)如图2.∵将△APC绕点C顺时针旋转60°,得到△EDC,
∴△APC≌△EDC,
∴∠ACP=∠ECD,AC=EC=5,∠PCD=60°,
∴∠ACP+∠PCB=∠ECD+∠PCB,
∴∠ECD+∠PCB=∠ACB=30°,
∴∠BCE=∠ECD+∠PCB+∠PCD=30°+60°=90°.
在Rt△BCE中,∵∠BCE=90°,BC=6,CE=5,
∴ ,
,
即PA+PB+PC的最小值为 ;
;
(2)①将△APC绕点C顺时针旋转60°,得到△DEC,连接PE.DE,则线段BD等于PA+PB+PC最小值的线段;

②当B.P.E.D四点共线时,PA+PB+PC值最小,最小值为BD.
∵将△APC绕点C顺时针旋转60°,得到△DEC,
∴△APC≌△DEC,
∴CP=CE,∠PCE=60°,
∴△PCE是等边三角形,
∴PE=CE=CP,∠EPC=∠CEP=60°.
∵菱形ABCD中,∠ABP=∠CBP= ∠ABC=30°,
∠ABC=30°,
∴∠PCB=∠EPC﹣∠CBP=60°﹣∠30°=30°,
∴∠PCB=∠CBP=30°,
∴BP=CP,
同理,DE=CE,
∴BP=PE=ED.
连接AC,交BD于点O,则AC⊥BD.
在Rt△BOC中,∵∠BOC=90°,∠OBC=30°,BC=4,
∴BO=BC•cos∠OBC= ,
,
∴BD=2BO= ,
,
∴BP= BD=
BD= .
.
即当PA+PB+PC值最小时PB的长为 .
.
考点:几何变换综合题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:阅读理解
| 61 |
| 61 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| A.①②④ | B.①⑤⑥ | C.②③⑥ | D.③④⑤ |
| A.陆琼的父亲陆云公接受梁武帝的诏令校定《棋品》,朱异、刘溉以下人员同时集中在一起,陆琼这时八岁,能在客人面前覆盘。 |
| B.天嘉元年,陆琼担任宁远始兴王府法曹行参军。不久以法曹行参军的身份兼任尚书外兵郎,任职期满由代理转为正职。 |
| C.陆琼生性谦虚俭朴,从不为自己聚敛财货。四时的俸禄,都散发给宗族人员,自己家中没有剩余财产。 |
| D.长沙王做江州刺史时,不遵循法度,高宗因为长沙王年少,派陆琼去做长史。陆琼前去担任了江州府国事,兼任寻阳太守。 |
查看答案和解析>>
科目:初中数学 来源:2012年北京市西城区中考数学二模试卷(解析版) 题型:解答题
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com