
【题目】一次函数的图象![]() 与两坐标轴围成的三角形的面积是8,且过点
与两坐标轴围成的三角形的面积是8,且过点![]() ,求此一次函数的解析式.
,求此一次函数的解析式.
【答案】![]() 或
或![]()
【解析】
先根据点![]() 求出b的值,再分
求出b的值,再分![]() 和
和![]() 两种情况,分别根据一次函数的图象特征、直角三角形的面积公式求出此函数与x轴的交点坐标,然后代入求解即可.
两种情况,分别根据一次函数的图象特征、直角三角形的面积公式求出此函数与x轴的交点坐标,然后代入求解即可.
由题意,将点![]() 代入
代入![]() 得:
得:![]()
则一次函数的解析式为![]()
由一次函数的定义可知,![]() ,因此,分以下两种情况讨论:
,因此,分以下两种情况讨论:
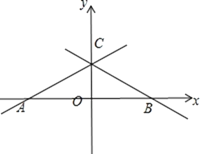
①![]() ,如图,设此时一次函数与x轴的交点为点B,与y轴的交点为点
,如图,设此时一次函数与x轴的交点为点B,与y轴的交点为点![]()
∵一次函数的图象![]() 与两坐标轴围成的三角形的面积是8
与两坐标轴围成的三角形的面积是8
∴![]() ,即
,即![]()
解得![]()
![]()
将点![]() 代入
代入![]() 得:
得:![]()
解得![]() ,符合题设
,符合题设
则此时一次函数的解析式为![]()
②![]() ,如图,设此时一次函数与x轴的交点为点A,与y轴的交点为点
,如图,设此时一次函数与x轴的交点为点A,与y轴的交点为点![]()
∵一次函数的图象![]() 与两坐标轴围成的三角形的面积是8
与两坐标轴围成的三角形的面积是8
∴![]() ,即
,即![]()
解得![]()
![]()
将点![]() 代入
代入![]() 得:
得:![]()
解得![]() ,符合题设
,符合题设
则此时一次函数的解析式为![]()
综上,此一次函数的解析式为![]() 或
或![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
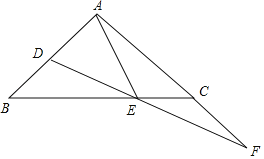
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.
(1)求证:DE=EF;
(2)判断BD和CF的数量关系,并说明理由;
(3)若AB=3,AE=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
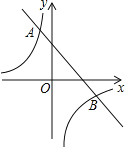
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2=![]() 的图象交于点A(﹣1,3)、B(n,﹣1).
的图象交于点A(﹣1,3)、B(n,﹣1).
(1)求反比例函数的解析式;
(2)当y1>y2时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC看,∠BAC=90°,AC=12,AB=10,D是AC上一个动点,以AD为直径的⊙O交BD于E,则线段CE的最小值是( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
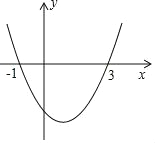
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3;③a+b+c<0;④当x>1时,y随x的增大而减小;⑤2a﹣b=0;⑥b2﹣4ac>0.下列结论一定成立的是( )
A. ①②④⑥ B. ①②③⑥ C. ②③④⑤⑥ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
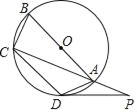
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(1)若AB=4,求![]() 的长;
的长;
(2)若![]() =
=![]() ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.

(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
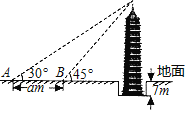
【题目】荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为_____米(![]() ≈1.73,结果精确到0.1).
≈1.73,结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
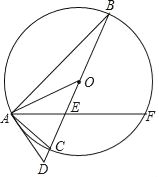
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,CE=2,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com