
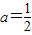 ,(6分)
,(6分)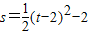 ,即
,即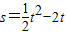 .
.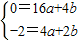 ,
,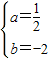
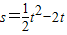 .
.

科目:初中数学 来源: 题型:
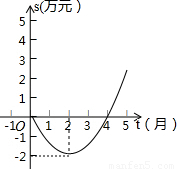
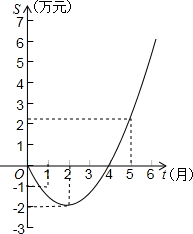 间的关系(即前t个月的利润总和S与t之间的关系).
间的关系(即前t个月的利润总和S与t之间的关系).查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
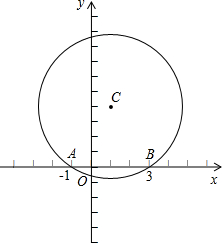 3,0)两点,且点C在x轴的上方.
3,0)两点,且点C在x轴的上方.查看答案和解析>>
科目:初中数学 来源: 题型:
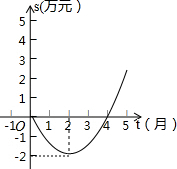 (2013•金平区模拟)如图的二次函数图象(部分)刻画了某公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
(2013•金平区模拟)如图的二次函数图象(部分)刻画了某公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
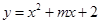 的图象与
的图象与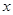 轴的正半轴交于点
轴的正半轴交于点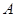 ,与
,与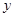 轴的正半轴交交于点
轴的正半轴交交于点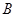 ,且
,且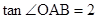 .设此二次函数图象的顶点为
.设此二次函数图象的顶点为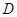 。
。
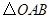 绕点
绕点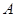 顺时针旋转
顺时针旋转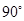 后,点
后,点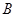 落到点
落到点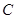 的位置.将上述二次函数图象沿
的位置.将上述二次函数图象沿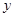 轴向上或向下平移后经过点
轴向上或向下平移后经过点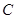 .请直接写出点
.请直接写出点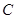 的坐标和平移后所得图象的函数解析式;
的坐标和平移后所得图象的函数解析式;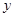 轴的交点为
轴的交点为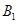 ,顶点为
,顶点为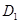 .点
.点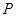 在平移后的二次函数图象上,且满足
在平移后的二次函数图象上,且满足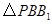 的面积是
的面积是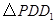 面积的
面积的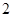 倍,求点
倍,求点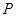 的坐标。
的坐标。查看答案和解析>>
科目:初中数学 来源:2011-2012年北京市第三十一中学九年级第一学期期中练习数学卷 题型:解答题
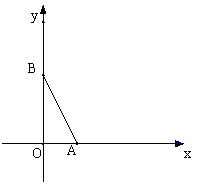
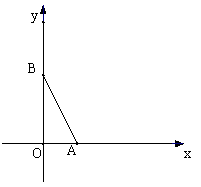
如图,在直角坐标系中,O为坐标原点,二次函数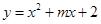 的图象与
的图象与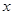 轴的正半轴交于点
轴的正半轴交于点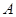 ,与
,与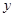 轴的正半轴交交于点
轴的正半轴交交于点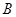 ,且
,且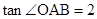 .设此二次函数图象的顶点为
.设此二次函数图象的顶点为 。
。
【小题1】(1)求这个二次函数的解析式;
【小题2】(2)将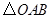 绕点
绕点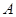 顺时针旋转
顺时针旋转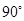 后,点
后,点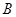 落到点
落到点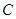 的位置.将上述二次函数图象沿
的位置.将上述二次函数图象沿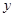 轴向上或向下平移后经过点
轴向上或向下平移后经过点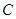 .请直接写出点
.请直接写出点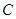 的坐标和平移后所得图象的函数解析式;
的坐标和平移后所得图象的函数解析式;
【小题3】(3)设(2)中平移后所得二次函数图象与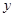 轴的交点为
轴的交点为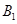 ,顶点为
,顶点为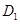 .点
.点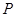 在平移后的二次函数图象上,且满足
在平移后的二次函数图象上,且满足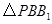 的面积是
的面积是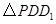 面积的
面积的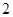 倍,求点
倍,求点 的坐标。
的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com