
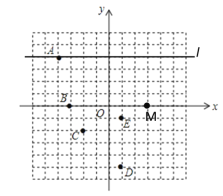
【题目】在平面直角坐标系中,每个小方格的边长为一个单位长度.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________;
的坐标为__________;
(2)点![]() 关于
关于![]() 轴对称点的坐标为__________;
轴对称点的坐标为__________;
(3)在直线![]() 上找一点
上找一点![]() ,使
,使![]() 为等腰三角形,点
为等腰三角形,点![]() 坐标为__________
坐标为__________
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)由平面直角坐标系即可写出点A、B的坐标;
(2)由平面直角坐标系即可写出点C的坐标,然后根据关于x轴对称的两点坐标关系:横坐标相同,纵坐标互为相反数即可得出结论;
(3)由平面直角坐标系可知:直线l上所有点的纵坐标为4,设N点坐标为(x,4),BM=6,然后根据等腰三角形腰的情况分类讨论,分别画出对应的图形,然后利用平面直角坐标系中任意两点之间的距离公式列方程即可.
解:(1)由平面直角坐标系可知:点A的坐标为(-4,4),点B的坐标为(-3,0)
故答案为:![]() ;
;![]() .
.
(2)由平面直角坐标系可知:点C的坐标为(-2,-2)
∴点![]() 关于
关于![]() 轴对称点的坐标为
轴对称点的坐标为![]()
故答案为:![]() ;
;
(3)由平面直角坐标系可知:直线l上所有点的纵坐标为4,设N点坐标为(x,4),BM=6
①当BN=BM时,以B为圆心BM的长为半径作圆,交直线l于两点N1和N2,如图所示
∴BN=![]()
解得:![]() ,
,![]()
∴N1的坐标为![]() ,N2的坐标为
,N2的坐标为![]() ;
;
②当MN=BM时,以M为圆心BM的长为半径作圆,交直线l于两点N3和N4,如图所示
∴MN=![]()
解得:![]() ,
,![]()
∴N3的坐标为![]() ,N2的坐标为
,N2的坐标为![]() ;
;
③当BN=MN时,点N在BM的中垂线上,由平面直角坐标系可知:y轴垂直平分BM
∴点N5为y轴与直线l的交点,如图所示
此时N5的坐标为![]() .
.

综上所述:点N1、N2、N3、N4、N5即为所求,符合题意的点N的坐标为![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]()
故答案为:![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年夏天,重庆各区持续高温日数达到历史之最,受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少,己知原有蓄水量![]() (万
(万![]() )与干旱持续时间
)与干旱持续时间![]() (天)的关系如图中线段
(天)的关系如图中线段![]() 所示,针对这种干旱情况,从第20天开始向水库注水,注水量
所示,针对这种干旱情况,从第20天开始向水库注水,注水量![]() (万
(万![]() )与时间
)与时间![]() (天)的关系如图中线段
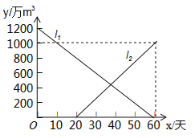
(天)的关系如图中线段![]() 所示(不考虑其他因素).若总蓄水量不多于900万
所示(不考虑其他因素).若总蓄水量不多于900万![]() 为严重干早,则该水库发生严重干旱共__________天
为严重干早,则该水库发生严重干旱共__________天
查看答案和解析>>
科目:初中数学 来源: 题型:
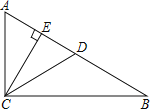
【题目】在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2![]() ,则AB=_____.
,则AB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作线段
作线段![]() 且
且![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)点![]() 的坐标轴__________,点
的坐标轴__________,点![]() 的坐标轴__________;
的坐标轴__________;
(2)直接写出点![]() 的坐标轴__________,并求出直线
的坐标轴__________,并求出直线![]() 的函数关系式;
的函数关系式;
(3)若点![]() 是图1中直线
是图1中直线![]() 上的一点,连接
上的一点,连接![]() ,得到图2,当点
,得到图2,当点![]() 在第二象限,且到
在第二象限,且到![]() 轴,
轴,![]() 轴的距离相等时,直接写出
轴的距离相等时,直接写出![]() 的面积;
的面积;
(4)若点![]() 是图1中坐标平面内不同于点
是图1中坐标平面内不同于点![]() 、点
、点![]() 的一点,当以点
的一点,当以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等时,直接写出点
全等时,直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的顶点都在网格的格点上(如图所示).
的顶点都在网格的格点上(如图所示).

(1)写出点![]() 的坐标____________,且该点到
的坐标____________,且该点到![]() 轴的距离为__________.
轴的距离为__________.
(2)作![]() 关于
关于![]() 轴的轴对称图形
轴的轴对称图形![]() .
.
(3)判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com