
【题目】 有一款如图(1)所示的健身器材,可通过调节AB的长度来调节椅子的高度,其平面示意图如图(2)所示,经测量,AD与DE的夹角为75°,AC与AD的夹角为45°,且DE∥AB.现调整AB的长度,当∠BCA为75°时测得点C到地面的距离为25cm.请求出此时AB的长度(结果保留根号).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,菱形 ABCD 的边 AD∥x 轴,直线y=2x+b 与 x 轴交于点 B,与反比例函数 y=![]() (k>0)图象交于点 D 和点 E,OB=3,OA=4.
(k>0)图象交于点 D 和点 E,OB=3,OA=4.
(1)求反比例函数和一次函数的解析式;
(2)点 P 为线段 BE 上的一个动点,过点 P 作 x 轴的平行线,当△CDE 被这条平行线分成面积相等的两部分时,求点 P 的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
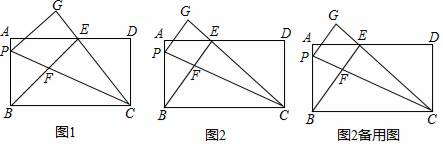
【题目】在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,①求证:BP=BF;
②当AD=25,且AE<DE时,求cos∠PCB的值;
③当BP=9时,求BEEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=﹣x2+bx+c经过点A(2,0)、B(0,2).
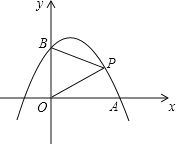
(1)求这条抛物线的解析式;
(2)如图,点P是抛物线上一动点,连接BP,OP,若△BOP是以BO为底边的等腰三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“农民也能报销医疗费了!”这是国家推行新型农村医疗合作的成果.村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可得到按一定比例返回的返回款,这一举措极大地增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了以下的统计图.
根据以上信息,解答以下问题:
(1)本次调查了 名村民,被调查的村民中,有 人参加合作医疗得到了返回款?
(2)若该乡有10000名村民,请你估计有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9680人,假设这两年的年平均增长率相同,求年平均增长率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,过
,过![]() 作直线
作直线![]() 交
交![]() 于另一点
于另一点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() 是直径
是直径![]() 上方半圆弧上一动点,
上方半圆弧上一动点,![]() 的半径为2,则
的半径为2,则
①当弦![]() 的长是 时,以
的长是 时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形;
为顶点的四边形是正方形;
②当![]() 的长度是 时,以
的长度是 时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形.
为顶点的四边形是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
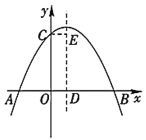
【题目】如图,抛物线![]() (
(![]() )与
)与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,抛物线的对称轴交
,抛物线的对称轴交![]() 轴于点
轴于点![]() ,
,![]() ,并与抛物线的对称轴交于点
,并与抛物线的对称轴交于点![]() .现有下列结论:①
.现有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中所有正确结论的序号是______.
.其中所有正确结论的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
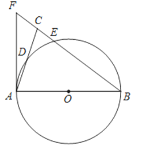
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.

(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com