
【题目】如图1,在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 是坐标轴上的一个点,若
是坐标轴上的一个点,若![]() 为直角边构造直角三角形
为直角边构造直角三角形![]() ,请求出满足条件的所有点
,请求出满足条件的所有点![]() 的坐标;
的坐标;
(3)如图 2,以点![]() 为直角顶点作
为直角顶点作![]() ,射线
,射线![]() 交
交![]() 轴的负半轴与点
轴的负半轴与点![]() ,射线
,射线![]() 交
交![]() 轴的负半轴与点
轴的负半轴与点![]() ,当
,当![]() 绕点
绕点![]() 旋转时,
旋转时,![]() 的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程) .
的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程) .

【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() 或
或![]() ;(3)8.
;(3)8.
【解析】
(1)由A、B两点的坐标利用待定系数法可求得直线AB的解析式;
(2)分别过A、B两点作AB的垂线,与坐标轴的交点即为所求的M点,再结合相似三角形的性质求得OM的长即可求得点M的坐标;
(3)过A分别作x轴和y轴的垂线,垂足分别为G、H,可证明![]() ,可得到
,可得到![]() ,从而可把OC-OD利用线段的和差转化为
,从而可把OC-OD利用线段的和差转化为![]() =8;
=8;
解:
(1)设直线![]() 的解析式为:
的解析式为:![]() .
.
![]() 点
点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,
![]()
![]() ,解得
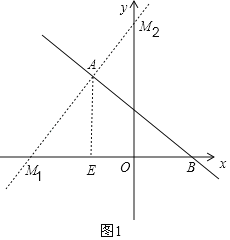
,解得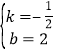 ,
,
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ;
;
(2)![]() 是以
是以![]() 为直角边的直角三角形,
为直角边的直角三角形,
![]() 有
有![]() 或
或![]() ,
,
①当![]() 时,如图1,
时,如图1,
过![]() 作
作![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
则可知![]() ,
,
![]()
![]() ,
,
由(1)可知![]() ,
,
![]()
![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,
轴,
![]()
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ;
;
②当![]() 时,如图2,
时,如图2,
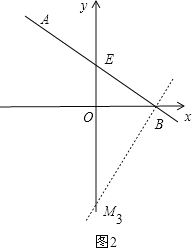
过![]() 作
作![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() ,
,
设直线![]() 交
交![]() 轴于点
轴于点![]() ,则由(1)可知
,则由(1)可知![]() ,
,
![]() ,
,![]() ,
,
由题意可知![]() △
△![]() ,
,
![]()
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,
,
综上可知点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() ;
;
(3)不变 .
理由如下:
过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,如图3.
,如图3.
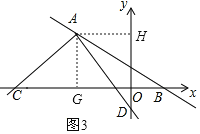
则![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中
中
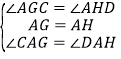 ,
,
![]() ,
,
![]() .
.
![]() .
.
故![]() 的值不发生变化,值为8.
的值不发生变化,值为8.


科目:初中数学 来源: 题型:
【题目】完成下面的证明:
已知:如图,点 D,E,F 分别在线段 AB,BC,AC 上,连接 DE、EF,DM 平分∠ADE 交 EF 于点 M,∠1+∠2=180°. 求证:∠B =∠BED.
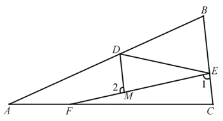
证明:∵∠1+∠2=180°(已知),
又∵∠1+∠BEM=180°(平角定义),
∴∠2=∠BEM( ),
∴DM∥ ( ).
∴∠ADM =∠B( ),
∠MDE =∠BED( ).
又∵DM 平分∠ADE (已知),
∴∠ADM =∠MDE (角平分线定义).
∴∠B =∠BED( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了普及环保知识,增强环保意识,某大学某专业学院从本专业450人中随机抽取了30名学生参加环保知识测试,得分![]() 十分制
十分制![]() 情况如图所示:
情况如图所示:
![]() 这30名学生的测试成绩的众数,中位数,平均数分别是多少?
这30名学生的测试成绩的众数,中位数,平均数分别是多少?
![]() 学院准备拿出2000元购买奖品奖励测试成绩优秀的学生,奖品分为三等,成绩为10分的为一等,成绩为8分和9分的为二等,成绩为7分的为三等;学院要求一等奖奖金,二等奖奖金,三等奖奖金分别占
学院准备拿出2000元购买奖品奖励测试成绩优秀的学生,奖品分为三等,成绩为10分的为一等,成绩为8分和9分的为二等,成绩为7分的为三等;学院要求一等奖奖金,二等奖奖金,三等奖奖金分别占![]() 、
、![]() 、
、![]() ,问每种奖品的单价各为多少元?
,问每种奖品的单价各为多少元?
![]() 如果该专业学院的学生全部参加测试,在
如果该专业学院的学生全部参加测试,在![]() 问的奖励方案下,请你预测该专业学院将会拿出多少奖金来奖励学生,其中一等奖奖金为多少元?
问的奖励方案下,请你预测该专业学院将会拿出多少奖金来奖励学生,其中一等奖奖金为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 和 CD 相交于点 O,∠C=∠COA,∠D=∠BOD.求证:AC∥BD.(补全下面的说理过程,并在括号内填上适当的理由)

证明:∵∠C=∠COA,∠D=∠BOD( )
又∠COA=∠BOD( )
∴∠C= .
∴AC∥BD.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,∠MON=80°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围.

(2)两条相交的直线OX、OY,使∠XOY=n,在射线OX、OY上分别再任意取A、B两点,作∠ABY的平分线BD,BD的反向延长线交∠OAB的平分线于点C,随着点A、B位置的变化,∠C的大小是否会变化?若保持不变,请求出∠C的度数;若发生变化,求出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)该校打算通过“京东商城”网购20个A品牌的足球和3个B品牌的足球,“五一”期间商城打折促销,其中A品牌打八折,B品牌打九折,问:学校购买打折后的足球所花的费用比打折前节省了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com