Question

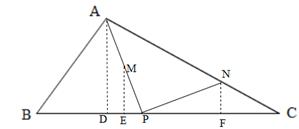
如图，△ABC中，AB=5，BC=11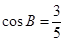，，点P是BC边上的一个动点，联结AP，取AP的中点M，将线段MP绕点P顺时针旋转90°得到线段PN，联结AN，NC.

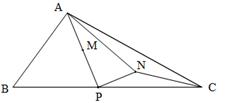
（1）当点N恰好落在BC边上时，求NC的长；

（2）若点N在△ABC内部（不含边界），设BP=x，CN=y，求y关于x的函数关系式，并求出函数的定义域；

（3）若△PNC是等腰三角形，求BP的长.

 

Answer 1

【答案】

（1）NC =6（2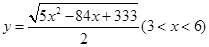）（3）BP = 7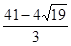或或．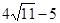

【解析】

试题分析：（1）根据三角函数定义求出BP，AP即可求出NC；

（2）过A作AD⊥BC于D，过M作ME⊥BC与E，过N作NF⊥BC于F，得到△MEP≌△PFN，利用三角函数定义，平行线的性质，求出ME，表示出EP，再由全等表示出NF，PF，FC，用勾股定理即可表示出NC；

（3）△PNC是等腰三角形，有三种可能：①PN=NC，②PN=PC，③PC=NC，表示出三边，解方程即可．

试题解析：（1）如图，当点N恰好落在BC边上时，AP⊥BC，∵AB=5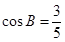，，∴BP=3，AB=4，∵M为AP的中点，∴AM=MP=2，∴PN=MP=2，∴NC=BC-BP-PN=11-3-2=6；

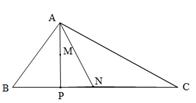
（2）过A作AD⊥BC于D，过M作ME⊥BC与E，过N作NF⊥BC于F，∵AB=5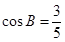，，∴BD=3，AD=4，

∵AD⊥BC，ME⊥BC，∴AD∥ME，∵M为AP的中点，BP=x，∴AM=MP，DE=EP，∴ME=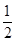AD=2，EP=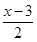，∵MP⊥NP，∴∠MPE+∠NPF=90°，∵∠MPE+∠PME=90°，∴∠PME=∠NPF，∵∠MEP=∠PFN=90°，MP=NP，∴△MEP≌△PFN，∴PF=ME=2，NF=EP=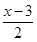，∴FC=BC-AP-PF=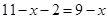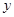，∴=NC=，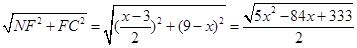

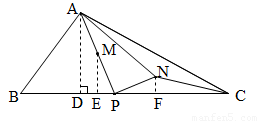
当N刚好在AC上时，如图，此时有DC=BC-BD=11-3=8，∵AD=4，∴DC=2AD，∵AD∥NF，∴DC：AD=FC：NF，∵NF=EP=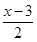，FC=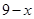，∴FC=2NF，∴，解得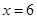：，∴定义域为：；

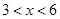（3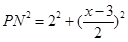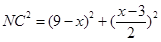），，PC=11-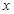，△PNC是等腰三角形，有三种可能：

①PN=NC，则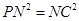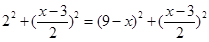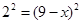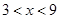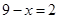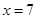，∴，∴，∵，∴，∴，∴BP=7；

②PN=PC，则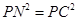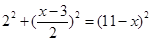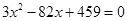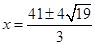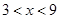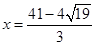，∴，∴，∴∵，∴，∴BP=；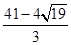

③PC=NC，则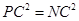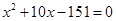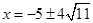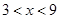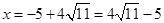，∴，∴，∴∵，∴，BP=．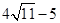

考点：三角形综合题．