
【题目】如图,ABCD的对角线AC、BD相交于点O.你能在图中找出几对全等的三角形?证明你的结论.
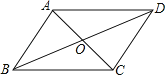
【答案】△AOB≌△COD,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA,证明见解析
【解析】
根据平行四边形性质可得,平行四边形对边相等,对角线互相平分,利用全等三角形判定定理(SSS)即可判定△AOB≌△COD,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA.
图中的全等三角形:△AOB≌△COD,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA,
∵四边形ABCD是平行四边形,
∴AB=CD,
在△AOB与△COD中,
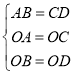
∴△AOB≌△COD(SSS).
∵四边形ABCD是平行四边形,
∴AD=BC,
在△AOD与△BOC中,
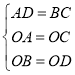
∴△AOD≌△COB(SSS).
∵四边形ABCD是平行四边形,
∴AB=CD ,AD=BC,
在△ABD与△CDB中,
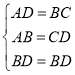
∴△ABD≌△CDB(SSS).
∵四边形ABCD是平行四边形,
∴AB=CD ,AD=BC,
在△ABC与ADC中,
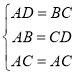
∴△ABC≌△CDA(SSS).


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
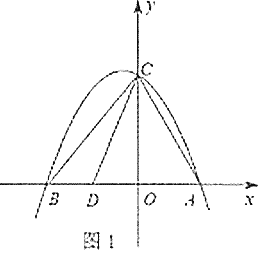
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() ,且点
,且点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() .
.
(1)如图2,点![]() 是直线
是直线![]() 上方抛物线上的一动点,在线段
上方抛物线上的一动点,在线段![]() 上有一动点
上有一动点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的最小值;
的最小值;
(2)将过点![]() 的直线
的直线![]() 绕点
绕点![]() 旋转,设旋转中的直线
旋转,设旋转中的直线![]() 分别与直线
分别与直线![]() 、直线
、直线![]() 交于点
交于点![]() 、
、![]() ,当
,当![]() 为等腰三角形时,直接写出
为等腰三角形时,直接写出![]() 的长.
的长.
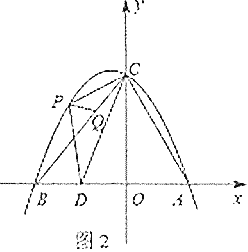
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某班甲、乙两名同学最近四次数学模拟考试成绩(满分150分)的条形统计图,则下列判断正确的是( )
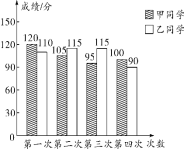
A.两名同学成绩的平均数相同
B.甲同学成绩的平均数比乙同学大
C.甲同学成绩的中位数比乙同学大
D.甲同学成绩的中位数比乙同学小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华文具店的某种毛笔每支售价![]() 元,书法练习本每本售价
元,书法练习本每本售价![]() 元,该文具店为促销制定了两种优惠办法:
元,该文具店为促销制定了两种优惠办法:
甲:买一支毛笔就赠送一本书法练习本;
乙:按购买金额打九折付款.
实验中学欲为校书法兴趣小组购买这种毛笔![]() 支,书法练习本
支,书法练习本![]()
![]() 本,
本,
(1)请写出用甲种优惠办法实际付款金额![]() 甲(元)与
甲(元)与![]() (本)之间的函数关系式;
(本)之间的函数关系式;
(2)请写出用乙种优惠办法实际付款金额![]() 乙(元)与
乙(元)与![]() (本)之间的函数关系式;
(本)之间的函数关系式;
(3)若购买同样多的书法练习本时,你会选择哪种优惠办法付款更省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
(1)求抛物线表达式;
(2)联结OP,当∠BOP=∠PBQ时,求PQ的长度;
(3)当△PBQ为等腰三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知二次函数图象与
中,已知二次函数图象与![]() 正半轴交于点
正半轴交于点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() .若过点
.若过点![]() 作平行于
作平行于![]() 轴的直线交抛物线于点
轴的直线交抛物线于点![]() .
.
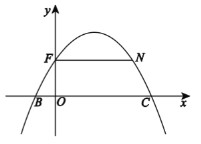
(1)点![]() 的横坐标为______;
的横坐标为______;
(2)设抛物线的顶点为点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,该二次函数有最大值3,试求
时,该二次函数有最大值3,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,我国的空气质量得到了大幅度的提高.现随机调查了某城市1个月的空气质量情况,并将监测的结果绘制成如下的两幅不完整的统计图.
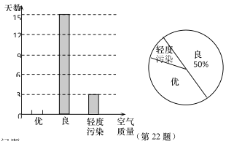
请根据图中提供的信息,解答下面的问题:
(1)本次调查中,一共调查的天数为_______天;扇形图中,表示“轻度污染”的扇形的圆心角为______度;
(2)将条形图补充完整;
(3)估计该城市一年(以365天计算)中,空气质量未达到优的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
例:若代数式![]() ,求a的取值.
,求a的取值.
解:原式=![]() ,
,
当a<2时,原式=(2-a)+(4-a)=6-2a=2,解得a=2(舍去);
当2≤a<4时,原式=(a-2)+(4-a)=2=2,等式恒成立;
当a≥4时,原式=(a-2)+(a-4)=2a-6=2,解得a=4;
所以,a的取值范围是2≤a≤4.
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
(1)当3≤a≤7时,化简:![]() =_________;
=_________;
(2)请直接写出满足![]() =5的a的取值范围__________;
=5的a的取值范围__________;
(3)若![]() =6,求a的取值.
=6,求a的取值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com