
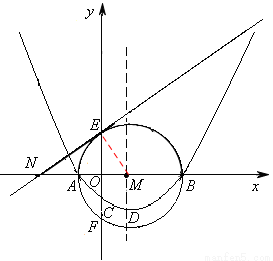
已知,如图(a),抛物线 经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°,
经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°,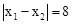 。
。
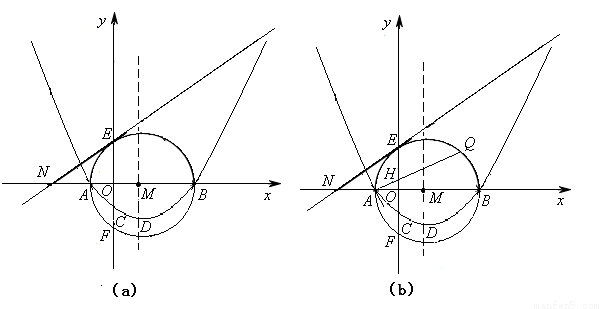
(1)求抛物线的解析式及顶点D的坐标;
(2)连结AD、BD,在(1)中的抛物线上是否存在一点P,使得△ABP与△ADB相似?若存在,求出P点的坐标;若不存在,说明理由;
(3)如图(b),点Q为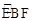 上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。
上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。
解:(1)圆的半径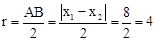 ,
,
连接EM,
∵NE是⊙M的切线,∴ME⊥NE。
在Rt△MNE中,∠ONE=30°,MA=ME=4,
∴∠EMN=60°,MN=8。∴OM=2。
∴OA=2,OB=6。
∴点A、B的坐标分别为(―2,0),(6,0)。
∵抛物线经过点A、B两点,
∴设抛物线的解析式为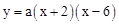 ,
,
又∵抛物线经过点C(0,-2),
∴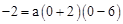 ,解得
,解得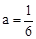 。
。
∴抛物线的解析式为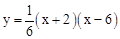 ,即
,即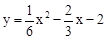 。
。
∵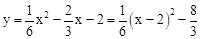 ,∴抛物线顶点D的坐标为(2,
,∴抛物线顶点D的坐标为(2,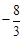 )。
)。
(2)如图,由抛物线的对称性可知:AD=BD,∠DAB=∠DBA。
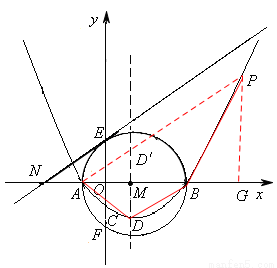
若在抛物线对称性的右侧图象上存在点P,使△ABP与△ADB相似,
必须有∠BAP=∠BPA=∠BPD。
设AP交抛物线的对称轴于D′点,则D′(2,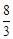 )。
)。
∴直线AP的解析式为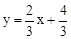 。
。
由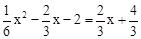 解得:
解得:
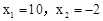 (舍去)。
(舍去)。
∴P(10,8)。
过P作PG⊥x轴于点G,
在Rt△BGP中,BG=4,PG=8,
∴由勾股定理,得PB=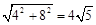 。
。
∵PA=8,∴PA≠PB。∴∠BAP≠∠BPA。
∴△ABP与△ADB不相似。
同理可说明在对称轴左边的抛物线上也不存在符合条件的P点。
∴在该抛物线上不存在点P,使得△ABP与△ADB相似。
(3)连接AF、QF,
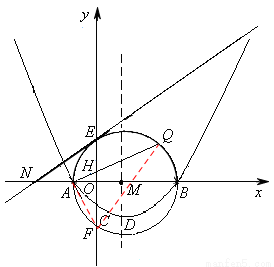
在△AQF和△AFH中,
由垂径定理易知: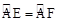 ,
,
∴∠AQF=∠AFH。
又∠QAF=∠HAF,
∴△AQF∽△AFH。
∴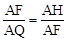 ,∴
,∴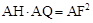 。
。
在Rt△AOF中,
 ,
,
∴AH·AQ=16,即:AH·AQ为定值
【解析】
试题分析:(1)由切线的性质和含30度角直角三角形的性质,求出点A、B的坐标,从而应用待定系数法求出抛物线的解析式,化为顶点式即可得到抛物线的顶点D的坐标。
(2)应用反证法分抛物线对称性的右侧和抛物线对称性的左侧两种情况说明在该抛物线上不存在点P,使得△ABP与△ADB相似。
(3)由垂径定理和相似三角形的判定和性质,可得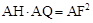 ,在Rt△AOF中,应用勾股定理可得
,在Rt△AOF中,应用勾股定理可得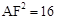 ,从而得出AH·AQ为定值的结论。
,从而得出AH·AQ为定值的结论。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| ||
| 2 |
 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:

|
| t(秒) | 1 | 2 | 3 | … |
| x(米) | 20 | 40 | 60 | … |
| Y(米) | 5 | 20 | 45 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
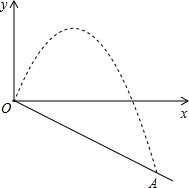 如图,东东站在斜坡OA上的O点处,向下抛出一块小石头,想看看自己能把小石头抛多远,已知他抛出小石头的运行路线可以用二次函数y=-
如图,东东站在斜坡OA上的O点处,向下抛出一块小石头,想看看自己能把小石头抛多远,已知他抛出小石头的运行路线可以用二次函数y=-| 9 |
| 16 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初三数学 华东师大(新课标2001/3年初审) 华东师大版 题型:044
已知,如图,在平面直角坐标系xOy中,抛物线l1的解析式为y=-x2,将抛物线l1平移后得到抛线物l2,若抛物线l2经过点(0,2),且其顶点A的横坐标为最小正整数.

(1)求抛物线l2的解析式;
(2)说明将抛物线l1如何平移得到抛物线l2;
(3)若将抛物线l2沿其对称轴继续上下平移,得到抛物线l3,设抛物线l3的顶点为B,直线OB与抛物线l3的另一个交点为C.当OB=OC时,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源:河南省期中题 题型:解答题
 中,抛物线
中,抛物线 的解析式为
的解析式为 ,将抛物线
,将抛物线 平移后得到抛线物
平移后得到抛线物 ,若抛物线
,若抛物线 经过点(0,2),且其顶点A的横坐标为最小正整数。
经过点(0,2),且其顶点A的横坐标为最小正整数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com