
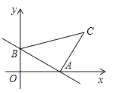
【题目】如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,以线段
,以线段![]() 为边在第一象限内作等腰
为边在第一象限内作等腰![]() ,
,![]() ,则过
,则过![]() 、
、![]() 两点直线的解析式为( )
两点直线的解析式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
易得OB=3,OA=4,由在等腰![]() 中,
中,![]() ,得AOBCDA(AAS),从而得C(7,4),进而根据待定系数法,即可得到答案.
,得AOBCDA(AAS),从而得C(7,4),进而根据待定系数法,即可得到答案.
∵一次函数![]() 的图象分别与
的图象分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,
,
∴A(4,0),B(0,3),
∴OB=3,OA=4,
过点C做CD⊥x轴于点D,
∵在等腰![]() 中,
中,![]() ,
,
∴∠OAB+∠CAD=∠OAB+∠ABO,即:∠CAD=∠ABO,
∵AB=AC,∠AOB=∠ADC=90°,
∴AOBCDA(AAS),
∴CD=AO=4,AD=BO=3,
∴C(7,4),
设直线![]()
![]() 的解析式为:y=kx+b,
的解析式为:y=kx+b,
把B(0,3),C(7,4),代入y=kx+b,得![]() ,解得:
,解得:![]() ,
,
∴直线![]()
![]() 的解析式为:y=
的解析式为:y=![]() x+3,
x+3,
故选A.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
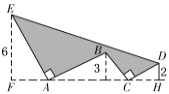
【题目】如图中,AE⊥AB且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6、3、2,则图中实线所围成的阴影部分面积S是( )
A.50B.44C.38D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用![]() 元购进某种干果后进行销售,由于销售状况良好,超市又调拨
元购进某种干果后进行销售,由于销售状况良好,超市又调拨![]() 元资金购进该种干果,购进干果的数量是第一次的
元资金购进该种干果,购进干果的数量是第一次的![]() 倍,但这次每干克的进价比第一次的进价提高了
倍,但这次每干克的进价比第一次的进价提高了![]() 元.
元.
(1)该种干果第一次的进价是每千克多少元?
(2)如果超市按每千克![]() 元的价格销售,当大部分干果售出后,余下的
元的价格销售,当大部分干果售出后,余下的![]() 千克按售价的
千克按售价的![]() 折售完,超市销售这种干果共盈利多少元?
折售完,超市销售这种干果共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
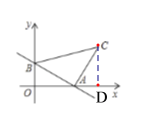
【题目】在△ABC中,AB=AC,∠BAC=![]() (
(![]() ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。

(1)如图1,直接写出∠ABD的大小(用含![]() 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°.
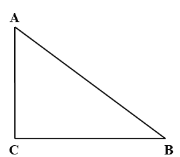
(1)作∠BAC的平分线,交BC于点D;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若BD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
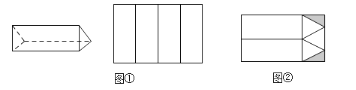
(1)若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?
(2)一共能生产多少个巧克力包装盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位后,再沿
个单位后,再沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() 称为第一次操作,把抛物线
称为第一次操作,把抛物线![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位后,再沿
个单位后,再沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() 称为第二次操作,…,以此类推,则抛物线
称为第二次操作,…,以此类推,则抛物线![]() 经过第
经过第![]() 此操作后得到的抛物线
此操作后得到的抛物线![]() 的解析式为( )
的解析式为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
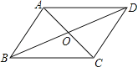
A.AB∥CD,AD∥BCB.OA=OC,OB=OD
C.AD=BC,AB∥CDD.AB=CD,AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com