
(已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE。

(1)求证:四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;
(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由。
(1)见解析;(2)24cm;(3)存在,过E作EP⊥AD交AC于P,则P就是所求的点,证明见解析.
【解析】
试题分析:(1)由四边形ABCD是矩形与折叠的性质,易证得△AOE≌△COF,即可得AE=CF,则可证得四边形AFCE是平行四边形,又由AC⊥EF,则可证得四边形AFCE是菱形;
由已知可得:S△ABF=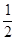 AB•BF=24cm2,则可得AB2+BF2=(AB+BF)2-2AB•BF=(AB+BF)2-2×48=AF2=100(cm2),则可求得AB+BF的值,继而求得△ABF的周长.
AB•BF=24cm2,则可得AB2+BF2=(AB+BF)2-2AB•BF=(AB+BF)2-2×48=AF2=100(cm2),则可求得AB+BF的值,继而求得△ABF的周长.
过E作EP⊥AD交AC于P,则P就是所求的点,首先证明四边形AFCE是菱形,然后根据题干条件证明△AOE∽△AEP,列出关系式.
试题解析:
(1)∵四边形ABCD是矩形,
∴AD∥BC,∴∠EAO=∠FCO,
由折叠的性质可得:OA=OC,AC⊥EF,
在△AOE和△COF中,
∵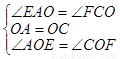 ,
,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵四边形AFCE是菱形,
∴AF=AE=10cm,
∵四边形ABCD是矩形,
∴∠B=90°,
∴S△ABF=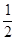 AB•BF=24cm2,
AB•BF=24cm2,
∴AB•BF=48(cm2),
∴AB2+BF2=(AB+BF)2-2AB•BF=(AB+BF)2-2×48=AF2=100(cm2),
∴AB+BF=14(cm)
∴△ABF的周长为:AB+BF+AF=14+10=24(cm).
(3)证明:过E作EP⊥AD交AC于P,则P就是所求的点.
当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在平行四边形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF,
∴OE=OF
∴四边形AFCE是菱形.
∴∠AOE=90°,又∠EAO=∠EAP,
由作法得∠AEP=90°,
∴△AOE∽△AEP,
∴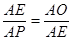 ,则AE2=A0•AP,
,则AE2=A0•AP,
∵四边形AFCE是菱形,
∴AO=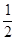 AC,
AC,
∴AE2=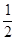 AC•AP,
AC•AP,
∴2AE2=AC•AP.
考点:1.翻折变换(折叠问题);2.菱形的判定;3.矩形的性质.


科目:初中数学 来源: 题型:
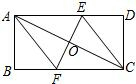 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.在线段AC上是否存在一点P,使得2AE2=AC•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.在线段AC上是否存在一点P,使得2AE2=AC•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
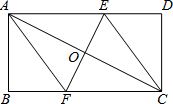 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•乐清市模拟)已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.
(2013•乐清市模拟)已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.求证:四边形AFCE是菱形.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.求证:四边形AFCE是菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com