
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴有两个交点
轴有两个交点![]() ,则下列说法正确的有:_________________.(填序号)
,则下列说法正确的有:_________________.(填序号)
①该二次函数的图象一定过定点![]() ;
;
②若该函数图象开口向下,则![]() 的取值范围为:
的取值范围为:![]() ;
;
③当![]() 且
且![]() 时,
时,![]() 的最大值为
的最大值为![]() ;
;
④当![]() 且该函数图象与
且该函数图象与![]() 轴两交点的横坐标
轴两交点的横坐标![]() 满足
满足![]() 时,
时,![]() 的取值范围为:
的取值范围为:![]() .
.
【答案】![]()
【解析】
根据二次函数图象与x轴有两个交点,利用根的判别式可求出![]() ,①中将点代入即可判断,②中根据“开口向下”和“与x轴有两个交点”即可得出m的取值范围,③中根据m的取值可判断出开口方向和对称轴范围,从而判断增减性确定最大值,④中根据开口方向及x1,x2的范围可判断出对应y的取值,从而建立不等式组求解集.
,①中将点代入即可判断,②中根据“开口向下”和“与x轴有两个交点”即可得出m的取值范围,③中根据m的取值可判断出开口方向和对称轴范围,从而判断增减性确定最大值,④中根据开口方向及x1,x2的范围可判断出对应y的取值,从而建立不等式组求解集.
由题目中![]() 可知:
可知:![]() ,
,![]() ,
,![]() ,
,
由题意二次函数图象与x轴有两个交点,则:
![]() ,即
,即![]() ,
,
①将![]() 代入二次函数解析式中,
代入二次函数解析式中,![]() ,则点
,则点![]() 在函数图象上,故正确;
在函数图象上,故正确;
②若二次函数开口向下,则![]() ,解得
,解得![]() ,且
,且![]() ,所以
,所以![]() 的取值范围为:
的取值范围为:![]() ,故正确;
,故正确;
③当![]() 时,
时,![]() ,即二次函数开口向上,对称轴
,即二次函数开口向上,对称轴![]() ,对称轴在
,对称轴在![]() 左侧,则当
左侧,则当![]() 时,
时,![]() 随
随![]() 的增大而增大,当
的增大而增大,当![]() 时有最大值,
时有最大值,![]() ,故错误;
,故错误;
④当![]() 时,
时,![]() ,即二次函数开口向上,
,即二次函数开口向上,
∵![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,即
,即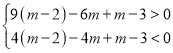 ,
,
解得:![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,即
,即![]() ,
,
解得:![]() ,
,
综上,![]() ,故正确.
,故正确.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了1元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2000元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3% 的损耗,第二次购进的水果有4% 的损耗,该水果店希望售完这些水果获利不低于3780元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班同学为了解某小区家庭月均用水情况(单位:吨),随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
25 | 2 | 0.04 |
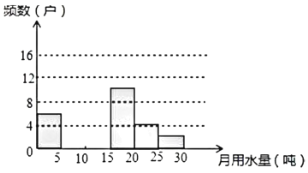
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区有1000户家庭,根据调查数据估计,该小区月均有水量超过20吨的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.矩形的对角线互相垂直平分
B.一组对角相等,一组对边平行的四边形一定是平行四边形
C.正八边形每个内角都是![]()
D.三角形三边垂直平分线交点到三角形三边距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受非洲猪瘟的影响,2019年的猪肉价格创历史新高,同时其他肉类的价格也有一定程度的上涨,某超市11月份的猪肉销量是羊肉销量的![]() 倍,且猪肉价格为每千克
倍,且猪肉价格为每千克![]() 元羊肉价格为每千克
元羊肉价格为每千克![]() 元.
元.
(1)若该超市11月份猪肉、羊肉的总销售额不低于![]() 万元,则11月份的猪肉销量至少多少千克?
万元,则11月份的猪肉销量至少多少千克?
(2)12月份香肠腊肉等传统美食的制作,使得市场的猪肉需求加大,12月份猪肉的销量比11月份增长了![]() ,由于国家对猪肉价格的调控,12 月份的猪肉价格比11月份降低了
,由于国家对猪肉价格的调控,12 月份的猪肉价格比11月份降低了![]() ,羊肉的销量是11月份猪肉销量的
,羊肉的销量是11月份猪肉销量的![]() ,且价格不变.最终,该超市12月份猪肉和.羊肉的销售额比11月份这两种肉的销售额增加了
,且价格不变.最终,该超市12月份猪肉和.羊肉的销售额比11月份这两种肉的销售额增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如下统计图.
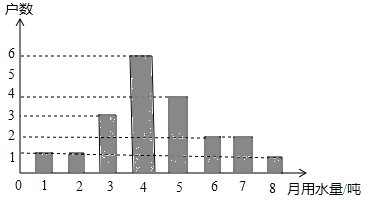
(1)小明一共调查了多少户家庭?
(2)所调查家庭5月份用水量的中位数、众数、平均数;
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
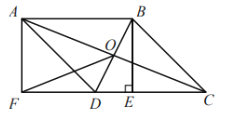
(1)求证:四边形ABEF是矩形;
(2)连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com