
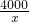 =
=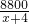 ,
,

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 的批发价买回一批畅销货.为了支付必要的开支,商店至少得赚回利润1100元,而为了保证这批新货迅速售完,不至于由畅销货变为滞销货,商店拟以低于零售价的价格,将这批新货卖出.设商店应该将这批新进货高出买进价的x%卖出,则
的批发价买回一批畅销货.为了支付必要的开支,商店至少得赚回利润1100元,而为了保证这批新货迅速售完,不至于由畅销货变为滞销货,商店拟以低于零售价的价格,将这批新货卖出.设商店应该将这批新进货高出买进价的x%卖出,则查看答案和解析>>
科目:初中数学 来源:2011年贵州省黔西南州中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com