
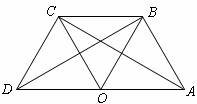
(1)如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.
求∠AEB的大小;
(2)如图,ΔOAB固定不动,保持ΔOCD的形状和大小不变,将ΔOCD绕着点O旋转(ΔOAB和ΔOCD不能重叠),求∠AEB的大小.

解:(1)如图
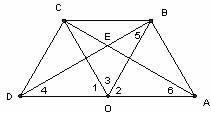
∵ △BOC和△ABO都是等边三角形,
且点O是线段AD的中点,
∴ OD=OC=OB=OA,∠1=∠2=60°,
∴ ∠4=∠5.
又∵∠4+∠5=∠2=60°,
∴ ∠4=30°
同理,∠6=30°.
∵ ∠AEB=∠4+∠6,
∴ ∠AEB=60°.
(2)如图.

∵ △BOC和△ABO都是等边三角形,
∴ OD=OC, OB=OA,∠1=∠2=60°,
又∵OD=OA,
∴ OD=OB,OA=OC,
∴ ∠4=∠5,∠6=∠7.
∵ ∠DOB=∠1+∠3,
∠AOC=∠2+∠3,
∴∠DOB=∠AOC.
∵ ∠4+∠5+∠DOB=180°, ∠6+∠7+∠AOC=180°,
∴ 2∠5=2∠6,
∴ ∠5=∠6
又∵ ∠AEB=∠8-∠5, ∠8=∠2+∠6,
∴ ∠AEB=∠2+∠5-∠5=∠2,
∴ ∠AEB=60°.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
 5、如图,点O是△ABC中∠ABC与∠ACB的平分线的交点,OD∥AB交BC于D点,OE∥AC交BC于E点,若BC=20cm,则△ODE的周长为( )
5、如图,点O是△ABC中∠ABC与∠ACB的平分线的交点,OD∥AB交BC于D点,OE∥AC交BC于E点,若BC=20cm,则△ODE的周长为( )查看答案和解析>>
科目:初中数学 来源: 题型:
 14、如图,点P是圆O的直径BC的延长线上一点,过点P作圆O的切线PA,切点为A,连接BA、OA、CA,过点A作AD⊥BC于D,请你找出图中共有
14、如图,点P是圆O的直径BC的延长线上一点,过点P作圆O的切线PA,切点为A,连接BA、OA、CA,过点A作AD⊥BC于D,请你找出图中共有查看答案和解析>>
科目:初中数学 来源: 题型:
 15、如图,点P是∠BAC的平分线上一点,PE⊥AB,PF⊥AC,E,F分别为垂足,①PE=PF,②AE=AF,③∠APE=∠APF,上述结论中正确的是
15、如图,点P是∠BAC的平分线上一点,PE⊥AB,PF⊥AC,E,F分别为垂足,①PE=PF,②AE=AF,③∠APE=∠APF,上述结论中正确的是查看答案和解析>>
科目:初中数学 来源: 题型:
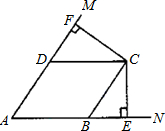 (2009•郑州模拟)如图,点C是∠MAN平分线上的一点,过点C作CF⊥AM于点F,CE⊥AN于点E,过点C作CD∥AN交AM于点D,CB∥AM交AN于点B.请你判断四边形ABCD是什么特殊的四边形?请说明理由.
(2009•郑州模拟)如图,点C是∠MAN平分线上的一点,过点C作CF⊥AM于点F,CE⊥AN于点E,过点C作CD∥AN交AM于点D,CB∥AM交AN于点B.请你判断四边形ABCD是什么特殊的四边形?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF∥BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.
说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF∥BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com