
【题目】下面是小明设计的“作平行四边形的高”的尺规作图过程
已知:平行四边形ABCD.
求作:![]() ,垂足为点E.
,垂足为点E.
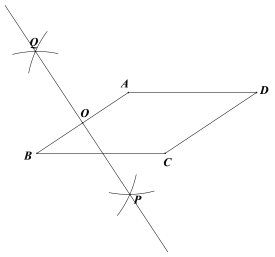
作法:如图,
①分别以点A和点B为圆心,大于![]() 的长为半径作弧,两弧相交于P,Q两点;
的长为半径作弧,两弧相交于P,Q两点;
②作直线PQ,交AB于点O;
③以点O为圆心,OA长为半径做圆,交线段BC于点E;
④连接AE.
所以线段AE就是所求作的高.
根据小明设计的尺规作图过程
⑴使用直尺和圆规,补全图形;(保留作图痕迹)
⑵完成下面的证明
证明:![]() AP=BP, AQ= ,
AP=BP, AQ= ,
![]() PQ为线段AB的垂直平分线.
PQ为线段AB的垂直平分线.
![]() O为AB中点.
O为AB中点.
![]() AB为直径,⊙O与线段BC交于点E,
AB为直径,⊙O与线段BC交于点E,
![]()
![]()
![]() .( )(填推理的依据)
.( )(填推理的依据)
![]()
![]() .
.
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
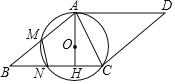
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.

(1)求直线![]() 和反比例函数
和反比例函数![]() 的解析式;
的解析式;
(2)已知点![]() 是反比例函数
是反比例函数![]() 图象上的一个动点,求点
图象上的一个动点,求点![]() 到直线
到直线![]() 距离最短时的坐标.
距离最短时的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
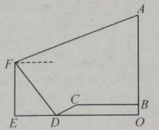
【题目】张华为了测量重庆最高塔楼![]() 的高度,他从塔楼底部
的高度,他从塔楼底部![]() 出发,沿广场前进185米至点
出发,沿广场前进185米至点![]() ,继而沿坡度为
,继而沿坡度为![]() 的斜坡向下走65米到达码头
的斜坡向下走65米到达码头![]() ,然后在浮桥上继续前行110米至趸船
,然后在浮桥上继续前行110米至趸船![]() ,在
,在![]() 处小明操作一架无人勘测机,当无人勘测机飞行至点
处小明操作一架无人勘测机,当无人勘测机飞行至点![]() 的正上方点
的正上方点![]() 时,测得码头
时,测得码头![]() 的俯角为
的俯角为![]() ,楼顶
,楼顶![]() 的仰角为
的仰角为![]() ,点
,点![]() 在同一平面内,则塔楼
在同一平面内,则塔楼![]() 的高度约为( )(结果精确到1米,参考数据:
的高度约为( )(结果精确到1米,参考数据:![]() ,
,![]() ,
,![]()
![]() )
)
A.319米B.335米C.342米D.356米
查看答案和解析>>
科目:初中数学 来源: 题型:
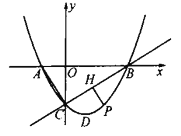
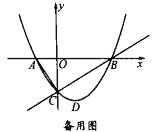
【题目】已知在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(1)如图,直线![]() 下方抛物线上的一个动点
下方抛物线上的一个动点![]() (不与点
(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 于点
于点![]() ,当
,当![]() 最大时,点
最大时,点![]() 为线段
为线段![]() 一点(不与点
一点(不与点![]() 重合),当
重合),当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标;
的坐标;
(2)将![]() 沿直线
沿直线![]() 翻折得
翻折得![]() ,再将
,再将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,在旋转过程中直线
,在旋转过程中直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法错误的是( )
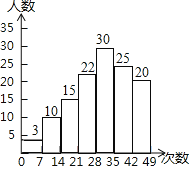
A.这栋居民楼共有居民125人
B.每周使用手机支付次数为28~35次的人数最多
C.有的人每周使用手机支付的次数在35~42次
D.每周使用手机支付不超过21次的有15人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com