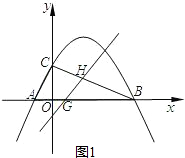
解:(1)∵∠ACB=90°,OC⊥AB,
∴△OAC∽△GCF.
∴
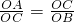
,即OC
2=OA•OB
∵OA:OB=1:4,OC=2
∴OA=1,OB=4
∴A(-1,0),B(4,0)
设抛物线的解析式是y=a(x+1)(x-4),
把C(0,2)坐标代入
得2=a(0+1)(0-4),a=-

,
∴抛物线的解析式是y=-

(x+1)(x+4)=-

x
2+

x+2.
(2)由B(4,0)、C(0,2)得直线BC解析式为y=-

x+2;
当直线y=x+b过点A时,b=1,由

,
得交点H(

,

),
则S
△ABH=

×5×

=

>

×5
S
△ACH=S
△ABC-S
△ABH=

<

×5
∴直线y=x+b只能与BC相交.
直线y=x+b与x轴交于点G(-b,0),BG=4+b,
解方程组
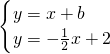
.
得H(

,

)
根据题意得

(4+b)×

=

×(

×5×2)
解得b=-1或b=-7

经检验,b=-7都是原方程的根,不符合题意舍去.
∴b=-1.
(3)根据题意得MQ∥OE,NQ∥OF
且MQ=OE=1,NQ=OF=2,
设M(t,
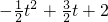
),
则N(t+2,

)
于是

-(

t)=1
∴M(1,3),N(2,1)
分析:(1)已知了OC的长,OA,OB的比例关系,可直接用射影定理求出OA,OB的长,即可得出A,B,C三点的坐标,然后用待定系数法求出抛物线的解析式.
(2)可先判断直线y=x+b与△ABC的哪个边相交,可求出直线过A点时,分△ABC的两部分的面积各为多少,以此可判断出直线与△ABC的哪条直角边相交,然后求出直线y=x+b与三角形两边的交点,然后根据直线分△ABC的两部分的面积来求出b的值.
(3)根据旋转的性质可知:MQ=OE,而MQ的值为M、N两点纵坐标的差,可据此来求两点的坐标.
点评:本题着重考查了待定系数法求二次函数解析式、图形旋转变换、三角形相似、函数图象的交点的求法,图形面积的求法等知识点,综合性强,能力要求较高.考查学生数形结合的数学思想方法.

 ,求b的值;
,求b的值;
 解:(1)∵∠ACB=90°,OC⊥AB,
解:(1)∵∠ACB=90°,OC⊥AB,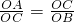 ,即OC2=OA•OB
,即OC2=OA•OB ,
, (x+1)(x+4)=-
(x+1)(x+4)=- x2+
x2+ x+2.
x+2. x+2;
x+2; ,
, ,
, ),
), ×5×
×5× =
= >
> ×5
×5 <
< ×5
×5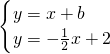 .
. ,
, )
) (4+b)×
(4+b)× =
= ×(
×( ×5×2)
×5×2)
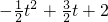 ),
), )
) -(
-( t)=1
t)=1

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案 (2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
(2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论: (2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为
(2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 的外接圆.
的外接圆. (2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.
(2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.