
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上的动点(含端点
上的动点(含端点![]() ,
,![]() ),连结
),连结![]() ,以
,以![]() 所在直线为对称轴作点
所在直线为对称轴作点![]() 的对称点
的对称点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() ,
,![]() 的中点,连结
的中点,连结![]() ,
,![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的长;
的长;
(3)以![]() 其中两边为邻边构造平行四边形,当所构造的平行四边形恰好是菱形时,这时该菱形的面积是________.
其中两边为邻边构造平行四边形,当所构造的平行四边形恰好是菱形时,这时该菱形的面积是________.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先利用三角形中位线定理得到![]() ,故
,故![]() ,可得四边形
,可得四边形![]() 为平行四边形,再根据对称性得到
为平行四边形,再根据对称性得到![]() ,即可得到
,即可得到![]() ,即邻边相等的平行四边形是菱形,故可求解;
,即邻边相等的平行四边形是菱形,故可求解;
(2)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,根据菱形的面积可求出
,根据菱形的面积可求出![]() ,再根据中位线及正方形的性质分别求出PN,PQ,CN,AQ,设
,再根据中位线及正方形的性质分别求出PN,PQ,CN,AQ,设![]() ,在
,在![]() 中,
中,![]() 得到方程求出x即可求解;
得到方程求出x即可求解;
(3)过点![]() 作
作![]() 的垂线,分别交
的垂线,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,分当
,分当![]() 时、当
时、当![]() 时、当
时、当![]() 时分别求出菱形的面积即可.
时分别求出菱形的面积即可.
解:(1)∵![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
∴四边形![]() 为平行四边形.
为平行四边形.
∵![]() 与
与![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为菱形.
为菱形.
(2)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,如图.
,如图.
![]() 四边形
四边形![]()
![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
设![]() ,
,
∴![]() .在
.在![]() 中,
中,![]() ,即
,即![]() ,
,
解得![]() ,
,
∴![]() .
.

(3)菱形的面积为![]() 或
或![]() 或
或![]() .理由如下:
.理由如下:
如图,过点![]() 作
作![]() 的垂线,分别交
的垂线,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
当![]() 时,点
时,点![]() 在点
在点![]() 处,
处,
此时![]() 菱形
菱形![]() ;
;
当![]() 时,此时
时,此时![]() 是正三角形,
是正三角形,
∴![]() ,PK=
,PK=![]() BP=5cm,
BP=5cm,
![]() 菱形
菱形![]() ;
;
当![]() 时,此时
时,此时![]() 是正三角形,
是正三角形,![]()
∴![]()
则CL=![]() CP=5cm,
CP=5cm,
∴![]() ,
,![]() ,
,
![]() 菱形
菱形![]() .
.
综上所述,菱形的面积为![]() 或
或![]() 或
或![]() .
.



 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,CD是![]() 的直径,弦AB⊥CD于点G,直线EF与
的直径,弦AB⊥CD于点G,直线EF与![]() 相切与点D,则下列结论中不一定正确的是
相切与点D,则下列结论中不一定正确的是
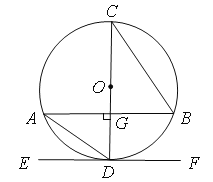
(A)AG=BG (B)AB∥EF (C)AD∥BC (D)∠ABC=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
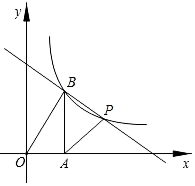
【题目】如图,在平面直角坐标系中,函数y=![]() 的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
(1)求k的值和点B的坐标.
(2)求直线BP的解析式.
(3)直接写出在第一象限内,使反比例函数大于一次函数的x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个白球,怎样估算白球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
统计结果如表:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到有记号球的次数m | 25 | 44 | 57 | 105 | 160 | 199 |
摸到有记号球的频率 | 0.25 | 0.22 | 0.19 | 0.21 | 0.20 | 0.20 |
(1)请你完成上表中数据,并估计摸到有记号球的概率是多少?
(2)估计盒中共有球多少个?没有记号球有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在做“抛掷一枚质地均匀的硬币”试验时,下列说法正确的是( )
A. 随着抛掷次数的增加,正面朝上的频率越来越小
B. 当抛掷的次数很大时,正面朝上的次数一定占总抛掷次数的![]()
C. 不同次数的试验,正面朝上的频率可能会不相同
D. 连续抛掷11次硬币都是正面朝上,第12次抛掷出现正面朝上的概率小于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋里装有2个相同的小球,它们分别写有数字1和2;乙口袋里装有3个相同的小球,它们分别写有数字3,4,5;丙口袋里有2个相同的小球,它们分别写有数字6,7,从三个口袋中各随机地取出1个小球,按要求解答下列问题:
(1)画出“树形图”;
(2)取出的3个小球上只有1个偶数数字的概率是多少?
(3)取出的3个小球上全是奇数数字的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).
(1)若点A在优弧![]() 上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com