练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是一个长为4，宽为3，高为12矩形牛奶盒，从上底一角的小圆孔插入一根到达底部的直吸管，吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)(　　)

    A. 5≤a≤12B. 12≤a≤3

    C. 12≤a≤4D. 12≤a≤13

    【答案】D

    【解析】

    最短距离就是牛奶盒的高度，当吸管、牛奶盒的高及底面对角线的长正好构成直角三角形时，插入盒子内的吸管长度最长，用勾股定理即可解答．

    最短距离就是牛奶盒的高度，即最短为12，

    由题意知：牛奶盒底面对角长为＝5，

    当吸管、牛奶盒的高及底面对角线的长正好构成直角三角形时，插入盒子内的吸管长度最长，

    则吸管长度为＝13，

    即吸管在盒内部分a的长度范围是12≤a≤13，

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】ABCD中，E是CD边上一点，
    （1）将△ADE绕点A按顺时针方向旋转，使AD、AB重合，得到△ABF，如图1所示．观察可知：与DE相等的线段是 ， ∠AFB=∠ .
    （2）如图2，正方形ABCD中，P、Q分别是BC、CD边上的点，且∠PAQ=45°，试通过旋转的方式说明：DQ+BP=PQ.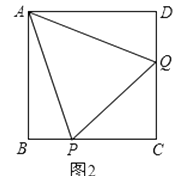
    （3）在（2）题中，连接BD分别交AP、AQ于M、N，你还能用旋转的思想说明BM2+DN2=MN2 ．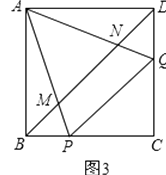

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣（x﹣1）2+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．

    （1）求点B，C的坐标；
    （2）判断△CDB的形状并说明理由；
    （3）将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点，点，点的坐标分别为，，．

    （1）将平移后得到，若点对应的点的坐标为，画出平移后的；

    （2）画出关于原点成中心对称的；

    （3）如果以，，，为顶点的四边形是平行四边形，请直接写出满足条件的所有点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单，为了尽快交货，增开了一条生产线，实际每月生产能力比原计划提高了50%，结果比原计划提前5个月完成交货，求每月实际生产智能手机多少万部．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形中，动点分别从两点同时出发，以相同的速度在直线上移动；

    (1)如图①,当分别移动到边的延长线上时，连接和与的关系为____ ；

    (2)如图②，己知正方形的边长为点和分别从点同时出发，以相同的速度沿方向向终点和运动，连接和，交于点，请你画出点运动路线的草图，试求出线段的最小值．

    (3)如图③，在(2)的条件下，求周长的最大值；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交 于点E，以点C为圆心，OA的长为直径作半圆交CE于点D．若OA=4，则图中阴影部分的面积为（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知AB//CD，点E为平面内一点，BE⊥CE于E

    （1）如图1，请直接写出∠ABE和∠DCE之间的数量关系

    （2）如图2，过点E作EF⊥CD，垂足为F，求证：∠CEF=∠ABE

    （3）如图3，在（2）的条件下，作EG平分∠CEF，交DF于点G，作ED平分∠BEF，交CD于D，连接BD，若∠DBE＋∠ABD＝180°，且∠BDE＝3∠GEF，求∠BEG的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，BA⊥MN，垂足为A，BA=4，点P是射线AN上的一个动点(不与点A重合)，∠BPC=∠BPA，BC⊥BP，过点C作CD⊥MN，垂足为D，设AP=x

    （1）CD的长度是否随着x的变化而变化？若变化，用含x的代数式表示CD的长度；若不变化，求出线段CD的长度；
    （2）△PBC的面积是否存在最小值？若存在，请求出这个最小值，并求出此时的x的值；若不存在，请说明理由；
    （3）当x取何值时，△ABP和△CDP相似；
    （4）如图2，当以C为圆心，以CP为半径的圆与线段AB有公共点时，求x的值。

    查看答案和解析>>

    同步练习册答案