
【题目】如图,在等边![]() 中,线段
中,线段![]() 为
为![]() 边上的中线.动点
边上的中线.动点![]() 在直线
在直线![]() 上时,以
上时,以![]() 为一边在
为一边在![]() 的下方作等边
的下方作等边![]() ,连结
,连结![]() .
.
(1)求![]() 的度数;
的度数;
(2)若点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() ;
;
(3)当动点![]() 在直线
在直线![]() 上时,设直线
上时,设直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,试判断
,试判断![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
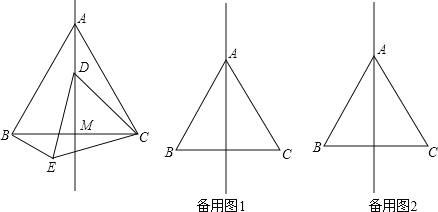
【答案】(1)30°;(2)证明见解析;(3)![]() 是定值,
是定值,![]() .
.
【解析】
(1)根据等边三角形的性质可以直接得出结论;
(2)根据等边三角形的性质就可以得出![]() ,
,![]() ,,
,,![]() ,由等式的性质就可以
,由等式的性质就可以![]() ,根据
,根据![]() 就可以得出
就可以得出![]() ;
;
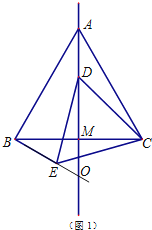
(3)分情况讨论:当点![]() 在线段
在线段![]() 上时,如图1,由(2)可知
上时,如图1,由(2)可知![]() ,就可以求出结论;当点
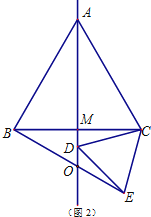
,就可以求出结论;当点![]() 在线段
在线段![]() 的延长线上时,如图2,可以得出
的延长线上时,如图2,可以得出![]() 而有
而有![]() 而得出结论;当点
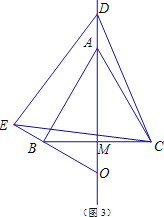
而得出结论;当点![]() 在线段
在线段![]() 的延长线上时,如图3,通过得出
的延长线上时,如图3,通过得出![]() 同样可以得出结论.
同样可以得出结论.
(1)![]() 是等边三角形,
是等边三角形,
![]() .
.
![]() 线段
线段![]() 为
为![]() 边上的中线,
边上的中线,
![]() ,
,
![]() .
.
(2)![]() 与
与![]() 都是等边三角形,
都是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中
中
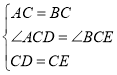 ,
,
![]() ;
;
(3)![]() 是定值,
是定值,![]() ,
,
理由如下:
①当点![]() 在线段
在线段![]() 上时,如图1,
上时,如图1,
由(2)可知![]() ,则
,则![]() ,
,
又![]() ,
,
![]() ,
,
![]() 是等边三角形,线段
是等边三角形,线段![]() 为
为![]() 边上的中线
边上的中线
![]() 平分
平分![]() ,即
,即![]()
![]() .
.
②当点![]() 在线段
在线段![]() 的延长线上时,如图2,
的延长线上时,如图2,
![]() 与
与![]() 都是等边三角形,
都是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
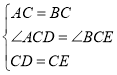 ,
,
![]() ,
,
![]() ,
,
同理可得:![]() ,
,
![]() .
.
③当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,
![]() 与
与![]() 都是等边三角形,
都是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
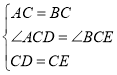 ,
,
![]() ,
,
![]() ,
,
同理可得:![]()
![]()
![]() ,
,
∵![]() ,
,
![]() .
.
综上,当动点![]() 在直线
在直线![]() 上时,
上时,![]() 是定值,
是定值,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.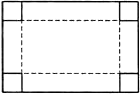
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】牛奶是最古老的天然饮料之一,被誉为“白色血液”,对人体的重要性可想而知,现已成为国家营养餐计划备选食品之一.为推行国家营养餐计划,某乳品公司向某营养餐中心运输一批牛奶,由铁路运输每千克只需运费0.58 元;由公路运输,每千克需运费0.28元,还需其他费用600元.请探究选用哪种运输方式所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com