
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交函数
轴的直线,交函数![]() 的图象于点
的图象于点![]() .
.
①当![]() 时,判断线段
时,判断线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
(3)设![]() ,
,![]() 是这个反比例函数图象上任意不重合的两点,
是这个反比例函数图象上任意不重合的两点,![]() ,
,![]() ,试判断
,试判断![]() ,
,![]() 的大小,并说明理由.
的大小,并说明理由.

【答案】(1)![]() 的值为3,
的值为3,![]() 的值为1;(2)①
的值为1;(2)①![]() ,详见解析;②
,详见解析;②![]() 或
或![]() ;(3)
;(3)![]() ,理由详见解析
,理由详见解析
【解析】
(1)![]() 代入直线
代入直线![]() 中求出m,然后再代入
中求出m,然后再代入![]() 中求出k即可;
中求出k即可;
(2)①把n=1代入,分别求出M,N的坐标,然后求出PM,PN长判断即可;
②根据![]() 分别表示出M和N的坐标,然后写出PM,PN长,根据
分别表示出M和N的坐标,然后写出PM,PN长,根据![]() 求出n的取值范围即可;
求出n的取值范围即可;
(3)![]() ,
,![]() 是这个反比例函数图象上任意不重合的两点,从而得到y1与x1、y2与x2的关系,然后只需运用作差法就可解决问题.
是这个反比例函数图象上任意不重合的两点,从而得到y1与x1、y2与x2的关系,然后只需运用作差法就可解决问题.
(1)![]() 函数
函数![]() 的图象与直线
的图象与直线![]() 交于
交于![]() ,
,
![]() ,
,
把![]() 代入
代入![]() 得,
得,
![]() ,
,
∴![]() 的值为3,
的值为3,![]() 的值为1;
的值为1;
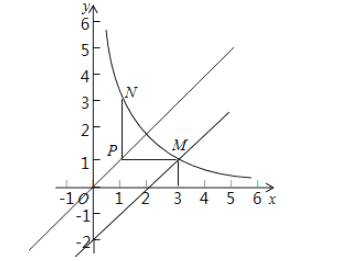
(2)①当![]() 时,
时,![]() ,
,
令![]() ,代入
,代入![]() 得
得![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() ,代入
,代入![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ;
;
②![]() ,点
,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,
,
∴![]() ,
,
∴PM=2,
∴N点坐标为![]() ,
,
∴PN=![]() ,
,
由题意知![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
∵n>0,
∴由![]() 解得:
解得:![]() ,
,
由![]() 解得:
解得:![]() ,
,
![]() 或
或![]() ;
;
(3)![]() ,理由如下:
,理由如下:
![]() ,
,![]() 是函数
是函数![]() 图象上的任意不重合的两点,
图象上的任意不重合的两点,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
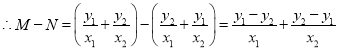
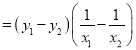
![]()
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)(x3)2.(﹣x4)3
(2)(![]() x5y4﹣
x5y4﹣![]() x4y3)
x4y3)![]() x3y3
x3y3
(3)(2a+1)2﹣(2a+1)(2a﹣1)
(4)102+![]() ×(π﹣3.14)0﹣|﹣302|
×(π﹣3.14)0﹣|﹣302|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要测量河宽,可在两岸找到相对的两点A、B,先从B出发与AB成90°方向向前走50米,到C处立一标杆,然后方向不变继续朝前走10米到D处,在D处转90°,沿DE方向走到E处,若A、C、E三点恰好在同一直线上,且DE=17米,你能根据题目提供的数据和图形求出河宽吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.
例如:由图1可得到(a+b)=a+2ab+b.
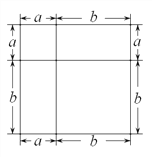
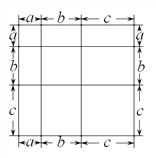
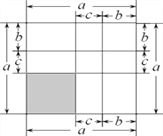
图1 图2 图3
(1)写出由图2所表示的数学等式:_____________________;写出由图3所表示的数学等式:_____________________;
(2)利用上述结论,解决下面问题:已知a+b+c=11,bc+ac+ab=38,求a+b+c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC>∠ADC,且∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E,则∠AEC与∠ADC、∠ABC 之间存在的等量关系是( )

A. ∠AEC=∠ABC﹣2∠ADC B. ∠AEC=![]()
C. ∠AEC= ![]() ∠ABC﹣∠ADC D. ∠AEC=
∠ABC﹣∠ADC D. ∠AEC= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB

(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的斜边![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 与原点重合,点
与原点重合,点![]() 的坐标是
的坐标是![]() ,且
,且![]() ,若将
,若将![]() 绕着点
绕着点![]() 旋转后30°,点
旋转后30°,点![]() 和
和![]() 点分别落在点
点分别落在点![]() 和点
和点![]() 处,那么直线
处,那么直线![]() 的解析式是__________.
的解析式是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3, 已知A(1,3),A1 (2,3), A2 (4,3), A3 (8,3),B(2,0), B1 (4,0), B2 (8,0), B3 (16,0),观察每次变换前后的三角形有何变化,找出规律,按此变换规律将△OA3B3变换成△OAnBn, ,则An的坐标是_______ ,Bn的坐标是_________ .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com