证:(1)过点P作GF∥AB,分别交AD、BC于G、F.如图所示.
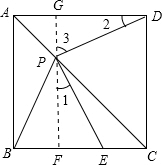
∵四边形ABCD是正方形,
∴四边形ABFG和四边形GFCD都是矩形,△AGP和△PFC都是等腰直角三角形,
∴GD=FC=FP,GP=AG=BF,∠PGD=∠PFE=90°;
又∵∠1+∠3=∠2+∠3=90°,
∴∠1=∠2;
又PF=GD,∠PFE=∠PGD=90°,
∴Rt△EFP≌Rt△PGD(ASA),
∴PE=PD;
(2)∵AD=AB,∠PAB=∠PAD=45°,AP=AP,
∴△APB≌△APD(SAS),
∴PB=PD,
∴PE=PB,
∴△PBE为等腰三角形;
(3)①∵AP=x,
∴
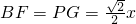
,
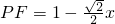
,
∴
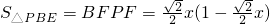
=

.
即
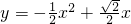
(
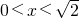
),
②
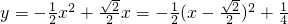
.
∵
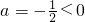
,
∴当

时,

.
分析:(1)作辅助线:过点P作GF∥AB,分别交AD、BC于G、F,构建全等三角形Rt△EFP≌Rt△PGD(ASA),然后由全等三角形的对应边相等证明PE=PD;
(2)由正方形的四条边相等,对角线平分对角的性质证明△APB≌△APD(SAS),然后由全等三角形的对应边相等证明PB=PD;利用(1)的结论,由等量代换证明PE=PB,即△PBE为等腰三角形;
(3)①利用△APB≌△APD的对应边相等知,BF=PG.在直角三角形AGP中,利用边角关系求得BF=PG的值,所以PF=AB-GP;然后根据三角形的面积公式求得关于y与x的函数关系式;
②根据①的函数关系式y=

x的顶点式函数关系式求最值.
点评:本题综合考查了二次函数的最值、正方形的性质、等腰三角形的性质及全等三角形的判定与性质.解答此题的关键是通过作辅助线:过点P作GF∥AB,分别交AD、BC于G、F,构建全等三角形Rt△EFP≌Rt△PGD(ASA),另外在求二次函数的最值时,在初中阶段一般情况下是将函数的一般解析式转化为顶点式函数解析式,然后根据函数的性质求其解析式.

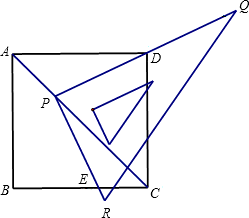 角线AC上移动,直角边PQ经过点D,另一直角边与射线BC交于点E.
角线AC上移动,直角边PQ经过点D,另一直角边与射线BC交于点E.
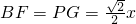 ,
,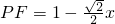 ,
,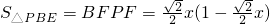 =
= .
.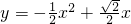 (
(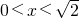 ),
),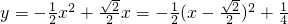 .
.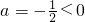 ,
, 时,
时, .
. x的顶点式函数关系式求最值.
x的顶点式函数关系式求最值.