
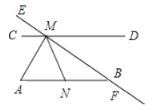
【题目】如图,∠CME+∠ABF=180°,MA平分∠CMN.若∠MNA=62°,求∠A的度数.根据提示将解题过程补充完整.
解:因为∠ABM+∠ABF=180°,
又因为∠CME+∠ABF=180°(已知),
所以∠ABM=∠CME
所以AB∥CD,理由:( )
所以∠CMN+( )=180°,
理由:(__________________________)
因为∠MNA=62°,
所以∠CMN=( )
因为MA平分∠CMN,
所以∠AMC=![]() ∠CMN =( ).(角平分线的定义)
∠CMN =( ).(角平分线的定义)
因为AB∥CD,
所以∠A=∠AMC=( )理由:(__________________________________)
【答案】同位角相等,两直线平行;∠MNA;两直线平行,同旁内角互补;118°;59°;59°;两直线平行,内错角相等
【解析】
根据同角的补角相等可得出∠ABM=∠CME,利用“同位角相等,两直线平行”可得出AB∥CD,由“两直线平行,同旁内角互补”及∠MNA =62°可求出∠CMN =118°,结合角平分线的定义可求出∠AMC的度数,再利用“两直线平行,内错角相等”即可求出∠A的度数.
解:因为∠ABM+∠ABF=180°,
又因为∠CME+∠ABF=180°(已知),
所以∠ABM=∠CME
所以AB∥CD,(同位角相等,两直线平行)
所以∠CMN+∠MNA=180°,(两直线平行,同旁内角互补)
因为∠MNA=62°,
所以∠CMN=118°,
因为MA平分∠CMN,
所以∠AMC=![]() ∠CMN =59°.(角平分线的定义)
∠CMN =59°.(角平分线的定义)
因为AB∥CD,
所以∠A=∠AMC=59°(两直线平行,内错角相等)
故答案为:同位角相等,两直线平行;∠MNA;两直线平行,同旁内角互补;118°;59°;59°;两直线平行,内错角相等


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB于点D,点E在CD上,下列四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④AC=EB,将其中两个作为条件,不能判定△ADC≌△EDB的是
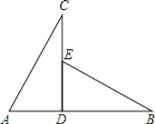
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图各图是棱长为1cm的小正方体摆成的,如图①中,从正面看有1个正方形,表面积为6cm2;如图②中,从正面看有3个正方形,表面积为18cm2;如图③,从正面看有6个正方形,表面积为36cm2;…
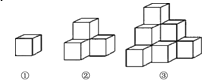
(1)第6个图中,从正面看有多少个正方形?表面积是多少?
(2)第n个图形中,从正面看有多少个正方形?表面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是_________.
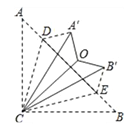
查看答案和解析>>
科目:初中数学 来源: 题型:
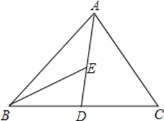
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
(1)若∠ABE=20°,∠BAD=45°,求∠BED的度数;
(2)画出△BED中BD边上的高;
(3)若△ABC的面积为80,BD=8,则点E到BC边的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点![]() 在数轴上分别对应的数为
在数轴上分别对应的数为![]() ,则
,则![]() 两点间的距离表示为
两点间的距离表示为![]() .
.
![]()
根据以上知识解题:
(1)若数轴上两点![]() 表示的数分别为
表示的数分别为![]() 、-1,
、-1,
①![]() 之间的距离可用含
之间的距离可用含![]() 的式子表示为 ;
的式子表示为 ;
②若该两点之间的距离为2,那么![]() 值为 .
值为 .
(2)![]() 的最小值为 ,此时
的最小值为 ,此时![]() 可以取的整数值是 .
可以取的整数值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,且BC=4,则△ABC 的面积为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )
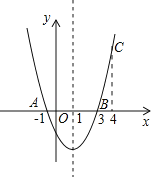
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com