
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпl1ЕФНтЮіЪНЮЊ![]() ЃЌжБЯпl2ЕФНтЮіЪНЮЊ
ЃЌжБЯпl2ЕФНтЮіЪНЮЊ![]() ЃЌгыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂЕуBЃЌжБЯпl1гыl2НЛгкЕуC.
ЃЌгыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂЕуBЃЌжБЯпl1гыl2НЛгкЕуC.
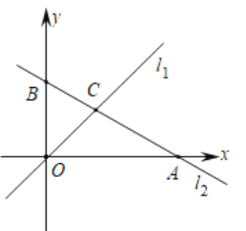

ЃЈ1ЃЉЧѓЕуAЁЂЕуBЁЂЕуCЕФзјБъЃЌВЂЧѓГіЁїCOBЕФУцЛ§ЃЛ
ЃЈ2ЃЉШєжБЯпl2ЩЯДцдкЕуPЃЈВЛгыBжиКЯЃЉЃЌТњзуSЁїCOP=SЁїCOBЃЌЧыЧѓГіЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкyжсгвВргавЛЖЏжБЯпЦНаагкyжсЃЌЗжБ№гыl1ЃЌl2НЛгкЕуMЁЂNЃЌЧвЕуMдкЕуNЕФЯТЗНЃЌyжсЩЯЪЧЗёДцдкЕуQЃЌЪЙЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіТњзуЬѕМўЕФЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉAЃЈ6ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌCЃЈ2ЃЌ2ЃЉЃЛУцЛ§ЮЊ3ЃЛЃЈ2ЃЉPЃЈ4ЃЌ1ЃЉЃЛЃЈ3ЃЉQЃЈ0ЃЌ![]() ЃЉЛђBЃЈ0ЃЌ
ЃЉЛђBЃЈ0ЃЌ![]() ЃЉЛђCЃЈ0ЃЌ
ЃЉЛђCЃЈ0ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩвЛДЮКЏЪ§НтЮіЪНЧѓГіЕуAЁЂBзјБъЃЌСЊСЂНтЮіЪННтЗНГЬзщЕУЕНЕу![]() ЃЛШЛКѓИљОн
ЃЛШЛКѓИљОн![]() ЕФУцЛ§
ЕФУцЛ§![]() ЃЌМДПЩЕУЕНШ§НЧаЮУцЛ§ЃЛ
ЃЌМДПЩЕУЕНШ§НЧаЮУцЛ§ЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌвРОнзјБъЯЕСНЕуОрРыЙЋЪНСаЗНГЬПЩЕУ
ЃЌвРОнзјБъЯЕСНЕуОрРыЙЋЪНСаЗНГЬПЩЕУ![]() ЃЌМДПЩЧѓНтЃЛ
ЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉЗж![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§жжЧщПіЃЌЗжБ№ЛГіЗћКЯЬѕМўЕФЭМаЮЃЌИљОнЯпЖЮЯрЕШЙиЯЕСаЗНГЬЧѓНтМДПЩЃЎ
Ш§жжЧщПіЃЌЗжБ№ЛГіЗћКЯЬѕМўЕФЭМаЮЃЌИљОнЯпЖЮЯрЕШЙиЯЕСаЗНГЬЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЕБx=0ЪБЃЌy=3ЃЌ
ЕБy=0ЪБЃЌ![]() ЃЌНтЕУЃКx=6ЃЌ
ЃЌНтЕУЃКx=6ЃЌ
Ёргы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№НЛгкЕу
жсЗжБ№НЛгкЕу![]() ЁЂЕу
ЁЂЕу![]() зјБъЗжБ№ЮЊ
зјБъЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
ЁпжБЯпl1гыl2НЛгкЕуC.
СЊСЂЕУЗНГЬзщЃК ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЙЪЕу![]() ЃЛ
ЃЛ
![]() ЕФУцЛ§
ЕФУцЛ§![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌ
ЃЌ
![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
НтЕУЃК![]() Лђ0ЃЈЩсШЅ
Лђ0ЃЈЩсШЅ![]() ЃЌ
ЃЌ
ЙЪЕу![]() ЃЛ
ЃЛ
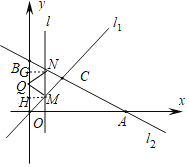
ЃЈ3ЃЉЩшЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФзјБъЗжБ№ЮЊ
ЕФзјБъЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
МДЃК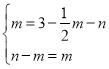 ЃЌ
ЃЌ
НтЕУЃК ЃЌ
ЃЌ
ЁрQЕузјБъЮЊЃК![]()
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ
дђ![]() ЃЌМДЃК
ЃЌМДЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЁрQЕузјБъЮЊЃК![]()
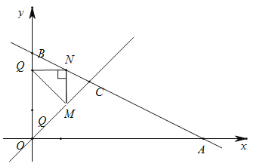
ЂлЕБ![]() ЪБЃЌ
ЪБЃЌ
ЭЌЂкРэПЩЕУЃК![]() ЃЛ
ЃЛ
ЁрQЕузјБъЮЊЃК![]()
злЩЯЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЗНГЬзщ![]() ЕФНтxЮЊЗЧе§Ъ§ЃЌyЮЊИКЪ§ЃЎ
ЕФНтxЮЊЗЧе§Ъ§ЃЌyЮЊИКЪ§ЃЎ
(1)ЧѓaЕФШЁжЕЗЖЮЇЃЛ
(2)ЛЏМђ|aЃ3|ЃЋ|aЃЋ2|ЃЛ
(3)дкaЕФШЁжЕЗЖЮЇжаЃЌЕБaЮЊКЮећЪ§ЪБЃЌВЛЕШЪН2axЃЋxЃО2aЃЋ1ЕФНтЮЊxЃМ1.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
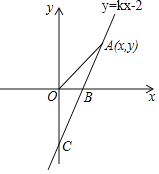
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНkxЉ2гыxжсЃЌyжсЗжБ№НЛгкBЃЌCСНЕуЃЌЦфжаOBЃН1ЃЎ
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉШєЕуAЃЈxЃЌyЃЉЪЧЕквЛЯѓЯоФкЕФжБЯпyЃНkxЉ2ЩЯЕФвЛИіЖЏЕуЃЌЕБЕуAдЫЖЏЙ§ГЬжаЃЌЪдаДГіЁїAOBЕФУцЛ§SгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЬНЫїЃК
ЂйЕБЕуAдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїAOBЕФУцЛ§ЪЧ1ЃЛ
ЂкдкЂйГЩСЂЕФЧщПіЯТЃЌxжсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁїPOAЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыаДГіТњзуЬѕМўЕФЫљгаPЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯ1+ЁЯ2ЃН180ЁуЃЌЁЯ3ЃНBЃЌ
ЃЈ1ЃЉжЄУїЃКEFЁЮABЃЎ
ЃЈ2ЃЉЪдХаЖЯЁЯAEDгыЁЯCЕФДѓаЁЙиЯЕЃЌВЂЫЕУїФуЕФРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгквЛдЊЖўДЮЗНГЬax2+bx+c=0ЃЈaЁй0ЃЉЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЂйШєaЃЌcвьКХЃЌдђЗНГЬax2+bx+c=0ЃЈaЁй0ЃЉвЛЖЈгаЪЕЪ§ИљЃЛ
ЂкШєb2Љ4acЃО0ЃЌдђЗНГЬax2+bx+c=0ЃЈaЁй0ЃЉвЛЖЈгаСНИіВЛЯрЕШЪЕЪ§ИљЃЛ
ЂлШєb=a+cЃЌдђЗНГЬax2+bx+c=0ЃЈaЁй0ЃЉгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ЂмШєЗНГЬax2+bx+c=0ЃЈaЁй0ЃЉЕФСНИљЗћКХЯрЭЌЃЌФЧУДЗНГЬcx2+bx+a=0ЃЈcЁй0ЃЉЕФСНИљЗћКХвВЯрЭЌЃЎ
A. жЛгаЂйЂл B. жЛгаЂйЂкЂм C. жЛгаЂйЂк D. жЛгаЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
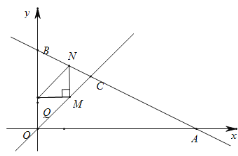
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЌBЕФзјБъЗжБ№ЮЊA(aЃЌ0)ЃЌB(bЃЌ0)ЃЌЧвaЃЌ
bТњзу |aЃЋ2|ЃЋ![]() ЃН0ЃЌЕуCЕФзјБъЮЊ(0ЃЌ3).
ЃН0ЃЌЕуCЕФзјБъЮЊ(0ЃЌ3).
ЃЈ1ЃЉЧѓaЃЌbЕФжЕМАSШ§НЧаЮABCЃЛ
ЃЈ2ЃЉШєЕуMдкxжсЩЯЃЌЧвSШ§НЧаЮACMЃН![]() SШ§НЧаЮABCЃЌЪдЧѓЕуMЕФзјБъ.
SШ§НЧаЮABCЃЌЪдЧѓЕуMЕФзјБъ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌаББп
ЃЌаББп![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌвд
ЕФжаЕуЃЌвд![]() ЮЊдВаФЃЌЯпЖЮ
ЮЊдВаФЃЌЯпЖЮ![]() ЕФГЄЮЊАыОЖЛдВаФНЧЮЊ
ЕФГЄЮЊАыОЖЛдВаФНЧЮЊ![]() ЕФЩШаЮ
ЕФЩШаЮ![]() ЃЌЛЁ
ЃЌЛЁ![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ________ЃЎ
ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжга![]() ЁЂ
ЁЂ![]() СНУЖОљдШЕФаЁСЂЗНЬхЃЈСЂЗНЬхЕФУПИіУцЩЯЗжБ№БъгаЪ§зж
СНУЖОљдШЕФаЁСЂЗНЬхЃЈСЂЗНЬхЕФУПИіУцЩЯЗжБ№БъгаЪ§зж![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЉЃЎгУаЁУїжР
ЃЉЃЎгУаЁУїжР![]() СЂЗНЬхГЏЩЯЕФЪ§зжЮЊ
СЂЗНЬхГЏЩЯЕФЪ§зжЮЊ![]() ЃЌаЁУїжР
ЃЌаЁУїжР![]() СЂЗНЬхГЏЩЯЕФЪ§зжЮЊ
СЂЗНЬхГЏЩЯЕФЪ§зжЮЊ![]() РДШЗЖЈЕу
РДШЗЖЈЕу![]() ЃЌдђаЁУїИїжРвЛДЮЫљШЗЖЈЕФЕу
ЃЌдђаЁУїИїжРвЛДЮЫљШЗЖЈЕФЕу![]() ТфдквбжЊХзЮяЯп
ТфдквбжЊХзЮяЯп![]() ЩЯЕФИХТЪЪЧ________ЃЎ
ЩЯЕФИХТЪЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЕк1Иі![]() жаЃЌ
жаЃЌ![]() ЃЛдкБп
ЃЛдкБп![]() ЩЯШЮШЁвЛЕу
ЩЯШЮШЁвЛЕу![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЕН
ЕН![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЕУЕНЕк2Иі
ЃЌЕУЕНЕк2Иі![]() ЃЛдкБп
ЃЛдкБп![]() ЩЯШЮШЁвЛЕу
ЩЯШЮШЁвЛЕу![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЕН
ЕН![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЕУЕНЕк3Иі
ЃЌЕУЕНЕк3Иі![]() ЁАДДЫзіЗЈМЬајЯТШЅЃЌдђЕк
ЁАДДЫзіЗЈМЬајЯТШЅЃЌдђЕк![]() ИіШ§НЧаЮжавд
ИіШ§НЧаЮжавд![]() ЮЊЖЅЕуЕФЕзНЧЖШЪ§ЪЧЃЈ ЃЉ
ЮЊЖЅЕуЕФЕзНЧЖШЪ§ЪЧЃЈ ЃЉ

A. B.
B. C.
C. D.
D.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com