
【题目】如图,在菱形ABCD中,tanA= ![]() ,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=
,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG= ![]() CG2;其中正确结论的序号为________.
CG2;其中正确结论的序号为________.
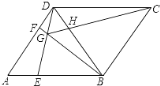
【答案】(1)(3)(4)
【解析】
(1)正确,先证明△ABD为等边三角形,根据“SAS”证明△AED≌△DFB;
(2)错误,只要证明△GDC≌△BGC,利用等腰三角形性质即可解决问题.
(3))正确,由△AED≌△DFB,推出∠ADE=∠DBF,所以∠BGE=∠BDG+∠DBG=∠BDG+∠ADE=60°,
(4)正确,证明∠BGE=60°=∠BCD,从而得点B、C、D、G四点共圆,因此∠BGC=∠DGC=60°,过点C作CM⊥GB于M,CN⊥GD于N.证明△CBM≌△CDN,所以S四边形BCDG=S四边形CMGN,易求后者的面积.
(1)∵四边形ABCD为菱形,
∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
在△AED和△DFB中,AE=DF,∠A=∠BDF,AD=BD,
∴△AED≌△DFB,故本小题正确;
(2)当点E,F分别是AB,AD中点时,
由(1)知,△ABD,△BDC为等边三角形,
∵点E,F分别是AB,AD中点,
∴∠BDE=∠DBG=30°,
∴DG=BG,
在△GDC与△BGC中,DG=BG,CG=CGC,D=CB,
∴△GDC≌△BGC,
∴∠DCG=∠BCG,
∴CH⊥BD,即CG⊥BD,故本选项错误;
(3)∵△AED≌△DFB,
∴∠ADE=∠DBF,
∴∠BGE=∠BDG+∠DBG=∠BDG+∠ADE=60°,故本选项正确.
(4)∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B. C. D. G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.过点C作CM⊥GB于M,CN⊥GD于N.(如图2) 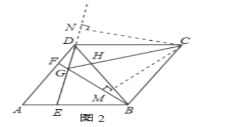
则△CBM≌△CDN,(AAS)
∴S四边形BCDG=S四边形CMGN,
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=![]() CG,CM=
CG,CM=![]() CG,
CG,
∴S四边形CMGN=2S△CMG=2×![]() ×
×![]() CG×
CG×![]() CG=
CG=![]() CG2,故本小题正确.
CG2,故本小题正确.
综上所述,正确的结论有(1)(3)(4).
故答案为:(1)(3)(4).


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
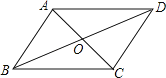
A.AB=CDB.AD∥BCC.OA=OCD.AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量y与单价x满足一次函数关系,求出y与x的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y=﹣![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() 上运动,则k的值为_____.
上运动,则k的值为_____.
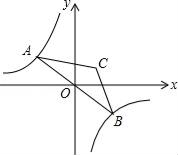
查看答案和解析>>
科目:初中数学 来源: 题型:
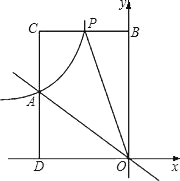
【题目】如图所示,正比例函数y=kx与反比例函数![]() 的图象交于点A(﹣3,2).
的图象交于点A(﹣3,2).
(1)试确定上述正比例函数与反比例函数的解析式;
(2)根据图象回答,在第二象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)P(m,n)是反比例函数图象上的一动点,其中﹣3<m<0,过点P作直线PB∥x轴,交y轴于点B,过点A作直线AD∥y轴,交x轴于点D,交直线PB于点C.当四边形OACP的面积为6时,请判断线段BP与CP的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设![]() ,
,![]() ,
,![]() ,请探索
,请探索![]() ,
,![]() ,
,![]() 满足的等量关系。
满足的等量关系。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
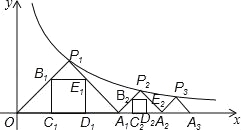
【题目】如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数y=![]() (x>0)的图象上,△P1OA,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数).若△P1OA1的内接正方形B1C1D1E1的周长记为l1,△P2A1A2的内接正方形的周长记为l2,…,△PnAn﹣1An的内接正方形BnCnDnEn的周长记为ln,则l1+l2+l3+…+ln= (用含n的式子表示).
(x>0)的图象上,△P1OA,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数).若△P1OA1的内接正方形B1C1D1E1的周长记为l1,△P2A1A2的内接正方形的周长记为l2,…,△PnAn﹣1An的内接正方形BnCnDnEn的周长记为ln,则l1+l2+l3+…+ln= (用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=3cm,AD=4cm,P从点A出发.以1cm/s的速度向点D匀速运动.设点P的运动时间为ts,问:四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com