
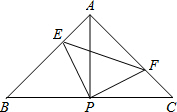
 如图,已知△ABC,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB、AC于E、F.下列结论:
如图,已知△ABC,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB、AC于E、F.下列结论: S△ABC.
S△ABC. PE,只有当PE⊥AB时,AP=
PE,只有当PE⊥AB时,AP= PE,AP=EF;再利用S△APE=S△CPF可得到S四边形AEPF=S△APC=
PE,AP=EF;再利用S△APE=S△CPF可得到S四边形AEPF=S△APC= S△ABC.
S△ABC.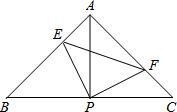
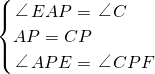 ,
, PE,
PE, PE,此时AP=EF,所以④错误;
PE,此时AP=EF,所以④错误; S△ABC,所以⑤正确.
S△ABC,所以⑤正确.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.
24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.
如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.查看答案和解析>>
科目:初中数学 来源: 题型:
 17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com