
 如图:以O为圆心的同心圆中,大圆的弦AB切小圆于C,AB=10cm,则圆环的面积是
如图:以O为圆心的同心圆中,大圆的弦AB切小圆于C,AB=10cm,则圆环的面积是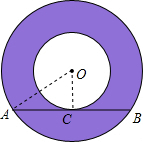
| 1 |
| 2 |


科目:初中数学 来源: 题型:
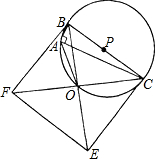 (1)求证:点O在⊙P上且∠BAO=135°;
(1)求证:点O在⊙P上且∠BAO=135°;| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AD |
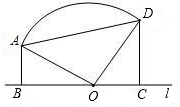
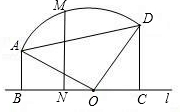
 |
| AD |
查看答案和解析>>
科目:初中数学 来源: 题型:044
如图,已知直线y = 2x(即直线![]() )和直线
)和直线![]() (即直线
(即直线![]() ),
),![]() 与x轴相交于点A。点P从原点O出发,向x轴的正方向作匀速运动,速度为每秒1个单位,同时点Q从A点出发,向x轴的负方向作匀速运动,速度为每秒2个单位。设运动了t秒.
与x轴相交于点A。点P从原点O出发,向x轴的正方向作匀速运动,速度为每秒1个单位,同时点Q从A点出发,向x轴的负方向作匀速运动,速度为每秒2个单位。设运动了t秒.
(1)求这时点P、Q的坐标(用t表示).
(2)过点P、Q分别作x轴的垂线,与![]() 、
、![]() 分别相交于点O1、O2(如图16).
分别相交于点O1、O2(如图16).
①以O1为圆心、O1P为半径的圆与以O2为圆心、O2Q为半径的圆能否相切?若能,求出t值;若不能,说明理由.
②以O1为圆心、P为一个顶点的正方形与以O2为中心、Q为一个顶点的正方形能否有无数个公共点?若能,求出t值;若不能,说明理由.(同学可在图中画草图)


查看答案和解析>>
科目:初中数学 来源: 题型:解答题
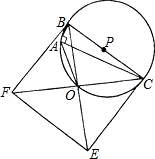 (1)求证:点O在⊙P上且∠BAO=135°;
(1)求证:点O在⊙P上且∠BAO=135°; ,求BO及AC的长.
,求BO及AC的长.查看答案和解析>>
科目:初中数学 来源:2007-2008学年江苏省苏州市常熟市九年级(上)期末数学试卷(解析版) 题型:解答题
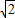 ,求BO及AC的长.
,求BO及AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com