
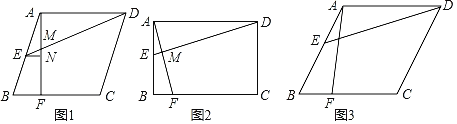
【题目】在平行四边形ABCD中,点E、F分别在边AB、BC上,DE、AF交于点M.
(1)如图1,E为AB的中点,AF⊥BC交BC于点F,过点E作EN⊥AF交AF于点N,![]() ,直接写出
,直接写出![]() 的值是 ;
的值是 ;
(2)如图2,∠B=90°,∠ADE=∠BAF,求证:△AEM∽△AFB;
(3)如图3,∠B=60°,AB=AD,∠ADE=∠BAF,求证:![]() .
.
【答案】(1)![]() ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
(1)证明EN∥BF,得出![]() ;
;
(2)证明四边形ABCD是矩形,得出∠BAD=∠ABC=90°,则∠AED=∠AFB,可得出结论;
(3)连接AC,过点B作BP∥AC交AF的延长线于点P,证明△BFP∽△CFA,得出![]() ,证明△ADE≌△BAP(ASA),得出AE=BP,则可得出结论.
,证明△ADE≌△BAP(ASA),得出AE=BP,则可得出结论.
解:(1)∵EN⊥AF,BF⊥AF,
∴EN∥BF,
又∵E为AB的中点,
∴BF=2EN,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(2)证明:∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,
∵∠ADE=∠BAF,
∴∠BAD﹣∠BAF=∠ABC﹣∠BAF
∴∠AED=∠AFB,
又∵∠BAF=∠MAE,
∴△AEM∽△AFB;
(3)证明:如图,连接AC,过点B作BP∥AC交AF的延长线于点P,
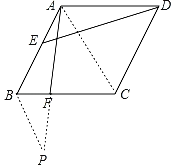
∴△BFP∽△CFA,
∴![]() ,
,
∵四边形ABCD是平行四边形,AB=AD,
∴四边形ABCD是菱形,
∵∠ABC=60°,
∴∠PBC=∠ACB=60°,
∴∠ABP=120°,
∴∠DAE=∠ABP,
在△ADE与△BAP中,
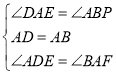 ,
,
∴△ADE≌△BAP(ASA),
∴AE=BP,
又∵AC=AD,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两公司为“见义勇为基金会”各捐款60000元,已知乙公司比甲公司人均多捐40元,甲公司的人数比乙公司的人数多20%.
请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
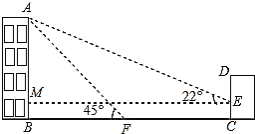
【题目】如图,某办公楼AB的右边有一建筑物CD,在建设物CD离地面2米高的点E处观测办公楼顶A点,测得的仰角![]() =
=![]() ,在离建设物CD 25米远的F点观测办公楼顶A点,测得的仰角
,在离建设物CD 25米远的F点观测办公楼顶A点,测得的仰角![]() =
=![]() (B,F,C在一条直线上).
(B,F,C在一条直线上).
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮晚上在广场散步,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.
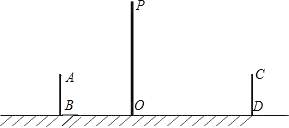
(1)请你在图中画出小亮站在AB处的影子BE;
(2)小亮的身高为1.6m,当小亮离开灯杆的距离OB为2.4m时,影长为1.2m,若小亮离开灯杆的距离OD=6m时,则小亮(CD)的影长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
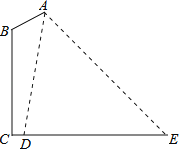
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,交y轴于点E.
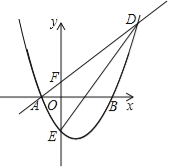
(1)求此抛物线的解析式.
(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时从![]() 地出发,沿同一路线各自匀速向
地出发,沿同一路线各自匀速向![]() 地行驶,甲到达
地行驶,甲到达![]() 地停留1小时后按原路以另一速度匀速返回,直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离
地停留1小时后按原路以另一速度匀速返回,直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离![]() (千米)与乙车行驶时间
(千米)与乙车行驶时间![]() (小时)之间的函数图象如图所示,则下列结论错误的是( )
(小时)之间的函数图象如图所示,则下列结论错误的是( )
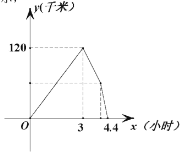
A.行驶3小时后,两车相距120千米
B.甲车从![]() 到
到![]() 的速度为100千米/小时
的速度为100千米/小时
C.甲车返回是行驶的速度为95千米/小时
D.![]() 、
、![]() 两地之间的距离为300千米
两地之间的距离为300千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,与反比例函数
两点,与反比例函数![]() 交于点
交于点![]() 点
点![]() 的坐标为
的坐标为![]() 轴于点
轴于点![]() .
.

(1)点![]() 的坐标为 ;
的坐标为 ;
(2)若点![]() 为
为![]() 的中点,求反比例函数
的中点,求反比例函数![]() 的解析式;
的解析式;
(3)在(2)条件下,以![]() 为边向右作正方形
为边向右作正方形![]() 交
交![]() 于点
于点![]() 直接写出
直接写出![]() 的周长与
的周长与![]() 的周长的比.
的周长的比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com