【答案】
分析:(1)根据已知条件构建平行四边形ADFE:延长AN到F,使MF=AM,连接DF、EF,由平行四边形的性质推出∠DAE+∠AEF=180°,再加上已知条件∠BAC+∠DAE=180°,不难知道∠BAC=∠AEF;而后根据已知线段间的比例关系,证明△ABC∽△EAF;最后利用相似三角形的性质来证明即可;
(2)选取①时,解题原理同(2);选取②时,先构建两个相似三角形△ABC与△AEF:如图,延长DA到F,使AF=AD,连接EF;然后证明两个三角形相似;最后由中位线的性质和相似三角形的性质来证明结论;
解答:
解:(1)∠ANB+∠BAE=180°.(1分)
证明:(法一)如图,延长AN到F,使MF=AM,连接DF、EF.(2分)
∵点M是DE的中点,∴DM=ME,∴四边形ADFE是平行四边形,(3分)
∴AD∥EF,AD=EF,∴∠DAE+∠AEF=180°,
∵∠BAC+∠DAE=180°,
∴∠BAC=∠AEF,(4分)
∵AB=kAE,AC=kAD,
∴

,∴

,(6分)
∴△ABC∽△EAF∴∠B=∠EAF,(8分)
∵∠ANB+∠B+∠BAF=180°,
∴∠ANB+∠EAF+∠BAF=180°,
即∠ANB+∠BAE=180°;(10分)

(法二)如图,延长DA到F,使AF=AD,连接EF.(2分)
∵∠BAC+∠DAE=180°,∠DAE+∠EAF=180°,
∴∠BAC=∠EAF,(3分)∵AB=kAE,AC=kAD,
∴
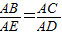
,∴

,(4分)
∴△ABC∽△AEF,(5分)
∴∠B=∠AEF,(6分)
∵点M是DE的中点,∴DM=ME,
又∵AF=AD,∴AM是△DEF的中位线,
∴AM∥EF,(7分)
∴∠NAE=∠AEF,
∴∠B=∠NAE,(8分)

∵∠ANB+∠B+∠BAN=180°,
∴∠ANB+∠NAE+∠BAN=180°,
即∠ANB+∠BAE=180°.(10分)
(2)不变化.如图(仅供参考),∠ANB=∠BAE.(12分)
选取(ⅰ),如图.

证明:延长AM到F,使MF=AM,连接DF、EF.
∵点M是DE的中点,
∴DM=ME,
∴四边形ADFE是平行四边形,(4分)
∴AD∥FE,AD=EF,∴∠DAE+∠AEF=180°,
∵∠BAC+∠DAE=180°,∴∠BAC=∠AEF,(6分)
∵AB=kAE,AC=kAD,k=1,∴AB=AE,AC=AD,
∴AC=EF,(7分)∴△ABC≌△EAF,∴∠B=∠EAF,(8分)
∵∠ANB+∠B+∠BAF=180°,∴∠ANB+∠EAF+∠BAF=180°,
即∠ANB+∠BAE=180°.(10分)
选取(ⅱ),如图.
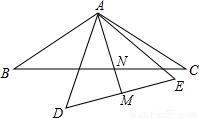
证明:∵AB=AC,∴∠B=

(180°-∠BAC),(3分)
∵∠BAC+∠DAE=180°,∴∠DAE=180°-∠BAC,
∴∠B=

∠DAE,∵AB=kAE,AC=kAD,
∴AE=AD,∵AM是△ADE的中线,AB=AC,
∴∠EAM=

∠DAE,∴∠B=∠EAM,(4分)
∵∠ANB+∠B+∠BAM=180°,∴∠ANB+∠EAM+∠BAM=180°,
即∠ANB+∠BAE=180°.(5分)
点评:本题主要考查的是相似三角形的判定与性质,三角形的中位线定理.


 解:(1)∠ANB+∠BAE=180°.(1分)
解:(1)∠ANB+∠BAE=180°.(1分) ,∴
,∴ ,(6分)
,(6分) (法二)如图,延长DA到F,使AF=AD,连接EF.(2分)
(法二)如图,延长DA到F,使AF=AD,连接EF.(2分)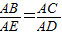 ,∴
,∴ ,(4分)
,(4分) ∵∠ANB+∠B+∠BAN=180°,
∵∠ANB+∠B+∠BAN=180°,

 (180°-∠BAC),(3分)
(180°-∠BAC),(3分) ∠DAE,∵AB=kAE,AC=kAD,
∠DAE,∵AB=kAE,AC=kAD, ∠DAE,∴∠B=∠EAM,(4分)
∠DAE,∴∠B=∠EAM,(4分)


