
����Ŀ����У��ȫ���ܵ�ȫ���Ĺ㷺��ע��ijУ���̴��Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ�����������������飬������ѧ���ijɼ�����ΪA����Ϥ����B�������˽⣩��C������֪������D��֪֮���٣��ĸ��ȴΣ����Ƴ���ͼ��ʾ������ͳ��ͼ��
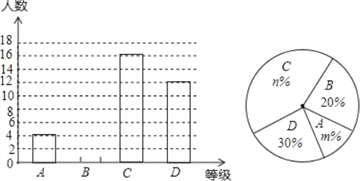
�����������Ϣ�ش��������⣺
��1���ֱ����ͳ��ͼ��m��n��ֵ��
��2�����Ƹ�У2350��ѧ����ΪA����Ϥ����B�������˽⣩���ε�ѧ�����ж����ˣ�
��3���ӱ�����ġ���Ϥ�����ε�ѧ���������ȡ2�ˣ��μ��оٰ��У��ȫ֪ʶ�����������б�����״ͼ
���𰸡���1��m=10��n=40����2��705���ˣ���3����A�ȼ���С���μӱ����ĸ���Ϊ��0.5��
����������������� ��1����D��12�ˣ�ռ30%������������������̶����m��n��ֵ����2������������������ķ�����������ô𰸣���3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ�����A�ȼ���С���μӱ���������������ø��ʹ�ʽ������ô𰸣�
�����������1����D��12�ˣ�ռ30%��
��У�12��30%=40���ˣ���
��n%=0.4��100%=40%��
��m%=1��20%��40%��30%=10%��
��m=10��n=40��
��2��2350����10%+20%��=705���ˣ���
��3���ֱ���A��B��C��ʾ�������ˣ�����״ͼ�ã�
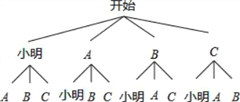
�߹���12�ֵȿ��ܵĽ������A�ȼ���С���μӱ�������6�������
���A�ȼ���С���μӱ����ĸ���Ϊ�� ![]() =0.5��
=0.5��


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ�����ͼ��Ķ��������ǣ���1����6�������Ҹ�ͼ���㣨2��3������ʽΪ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼��У�����¼��ǣ� ��
A.̫�����ŵ���ת
B.С���ﳵ����ij��ʮ��·��ʱ�������
C.�����Ϻ����������½�����
D.һ������37��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ε����߳��ֱ�Ϊ6 �M��9 cm����������ߵij�����Ϊ
A. 2�M B. 3 cm C. 7�M D. 16 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ABC�ǵ���ֱ�������Σ���BAC=90�㣬AB=AC���ı���ADEF�������Σ���B��C�ֱ���AD��AF�ϣ���ʱBD=CF��BD��CF������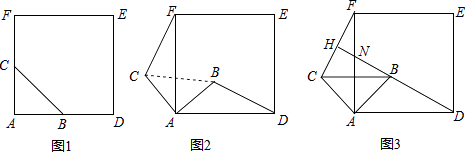
��1����ͼ�ڣ�
i������ABC�Ƶ�A��ʱ����ת�ȣ�0�㣼�ȣ�90�㣩ʱ���߶�BD���߶�CF��������ϵ����ֱ��BD��ֱ��CF��λ�ù�ϵ�� ��
ii��������ͼ��֤���������ۣ�
��2����ͼ�ۣ�����ABC�Ƶ�A��ʱ����ת45��ʱ���ӳ�DB��CF�ڵ�H����AB= ![]() ��AD=3ʱ�����߶�FC�ij���
��AD=3ʱ�����߶�FC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=3��BC=4��CD=12��AD=13����B=90�㣬���ı���ABCD������ǣ������� 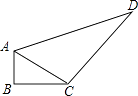
A.36
B.40
C.![]()
D.38
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ε������߷ֱ�Ϊ6��8������������ε��ܳ��ǣ� ��
A. 20 B. 22 C. 20��22 D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AN����M��ֱ����NB��x�ᣬAB����M�ڵ�C��
��1������A��0��6����N��0��2������ABN=30�㣬���B�����ꣻ
��2����DΪ�߶�NB���е㣬��֤��ֱ��CD����M�����ߣ�
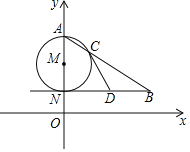
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У���ABC=45�㣬E��F�ֱ���CD��BC���ӳ����ϣ�AE��BD��EF��BC��AB=1����EF�ij��ǣ� �� 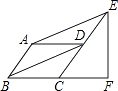
A.1.5
B.![]()
C.![]()
D.2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com