
【题目】在![]() 中,
中,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),以
重合),以![]() 为腰作等腰直角
为腰作等腰直角![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)观察猜想
如图1,当点![]() 在线段
在线段![]() 上时,
上时,
①![]() 与
与![]() 的位置关系为__________;
的位置关系为__________;
②![]() 之间的数量关系为___________(提示:可证
之间的数量关系为___________(提示:可证![]() )
)

(2)数学思考
如图2,当点![]() 在线段
在线段![]() 的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)拓展延伸
如图3,当点![]() 在线段
在线段![]() 的延长线时,将
的延长线时,将![]() 沿线段
沿线段![]() 翻折,使点
翻折,使点![]() 与点
与点![]() 重合,连接
重合,连接![]() ,若
,若![]() ,请直接写出线段
,请直接写出线段![]() 的长.(提示:做
的长.(提示:做![]() 于
于![]() ,做
,做![]() 于
于![]() )
)
【答案】(1)①BC⊥CF;②BC=CF+DC;(2)C⊥CF成立;BC=CF+DC不成立,正确结论:DC=CF+BC,证明详见解析;(3)![]()
【解析】
(1)①根据正方形的性质得,∠BAC=∠DAF=90°,推出△DAB≌△FAC(SAS);②由正方形ADEF的性质可推出△DAB≌△FAC,根据全等三角形的性质可得到![]() ,
,![]() ,根据余角的性质即可得到结论;
,根据余角的性质即可得到结论;
(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质以及等腰三角形的角的性质可得到结论;
(3)过A作![]() 于H,过E作
于H,过E作![]() 于M,证明
于M,证明![]() ,推出
,推出![]() ,
,![]() ,推出
,推出![]() ,即可解决问题.
,即可解决问题.
(1)①正方形ADEF中,![]()
∵![]()
∴![]()
在△DAB与△FAC中
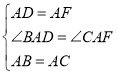
∴![]()
∴![]()
∴![]() ,即
,即![]() ;
;
②∵![]()
∴![]()
∵![]()
∴![]()
(2)BC⊥CF成立;BC=CF+DC不成立,正确结论:DC=CF+BC
证明:∵△ABC和△ADF都是等腰直角三角形
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∴∠BAD=∠CAF
在△DAB和△FAC中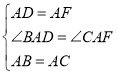
∴△DAB≌△FAC(SAS)
∴∠ABD=∠ACF,DB=CF
∵∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°
∴∠ABD=180°-45°=135°
∴∠ACF=∠ABD=135°
∴∠BCF=∠ACF-∠ACB=135°-45°=90°,
∴CF⊥BC
∵CD=DB+BC,DB=CF
∴DC=CF+BC
(3)过A作![]() 于H,过E作
于H,过E作![]() 于M,
于M,
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵四边形ADEF是正方形
∴![]()
∵![]()
∴四边形CMEN是矩形
∴![]()
∵![]()
∴![]()
∴![]()
在△ADH和△DEM中
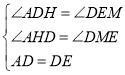
∴![]()
∴![]()
∴![]()
∴![]()


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】矩形OABC在平面直角坐标系中的位置如图所示,已知![]() ,点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作
,点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作![]() ,交x轴于点D.下列结论:①
,交x轴于点D.下列结论:①![]() ;②当点D运动到OA的中点处时,
;②当点D运动到OA的中点处时,![]() ;③在运动过程中,
;③在运动过程中,![]() 是一个定值;④当△ODP为等腰三角形时,点D的坐标为
是一个定值;④当△ODP为等腰三角形时,点D的坐标为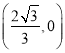 .其中正确结论的个数是( )
.其中正确结论的个数是( )
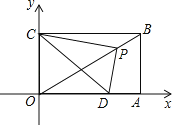
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
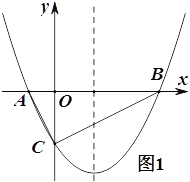
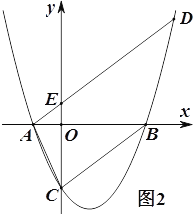
【题目】如图,已知抛物线![]() (
(![]() >0)与
>0)与![]() 轴交于A,B两点(A点在B点的左边),与
轴交于A,B两点(A点在B点的左边),与![]() 轴交于点C。
轴交于点C。
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
(2)如图1,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B,C,P,Q为顶点的四边形是平行四边形,求P点的坐标;
(3)如图2,过点A作直线BC的平行线交抛物线于另一点D,交![]() 轴交于点E,若AE:ED=1:4,求
轴交于点E,若AE:ED=1:4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第1次操作,折痕
处,称为第1次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,还原纸片后,再将
,还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第2次操作,折痕
处,称为第2次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,按上述方法不断操作下去…经过第2020次操作后得到的折痕
,按上述方法不断操作下去…经过第2020次操作后得到的折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
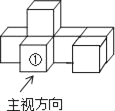
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
科目:初中数学 来源: 题型:
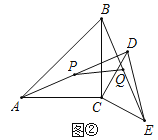
【题目】如图1,![]() ,
,![]() ,
,![]() ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM.![]() 求证:
求证:![]() ;
;![]() 求
求![]() 的度数
的度数![]() 用含
用含![]() 的式子表示
的式子表示![]() ;
;![]() 如图2,当
如图2,当![]() 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断![]() 的形状,并加以证明.
的形状,并加以证明.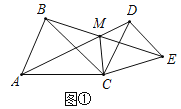
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com