
| 苹果品种 | 甲 | 乙 | 丙 |
| 每吨苹果所获利润(万元) | 0.22 | 0.21 | 0.20 |


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源:2010年浙江省杭州市萧山区中考数学模拟试卷32(新湾初中 薛源海)(解析版) 题型:解答题
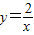 和
和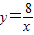 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与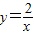 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与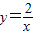 ,
,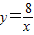 的图象交于点C、D.
的图象交于点C、D.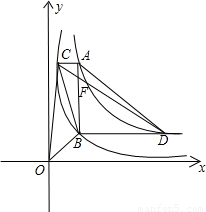
查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市文澜中学中考数学模拟试卷(解析版) 题型:解答题
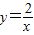 和
和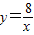 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在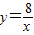 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与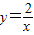 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与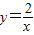 ,
,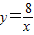 的图象交于点C、D.
的图象交于点C、D.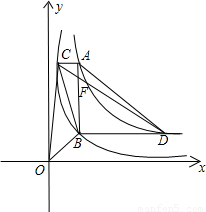
查看答案和解析>>
科目:初中数学 来源:2010年吉林省珲春市珲春四中中考数学模拟试卷(解析版) 题型:解答题
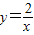 和
和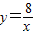 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在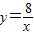 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与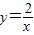 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与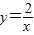 ,
, 的图象交于点C、D.
的图象交于点C、D.
查看答案和解析>>
科目:初中数学 来源:2009年江苏省泰州市泰兴市济川实验初中中考数学二模试卷(解析版) 题型:解答题
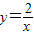 和
和 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在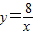 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与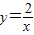 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与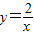 ,
, 的图象交于点C、D.
的图象交于点C、D.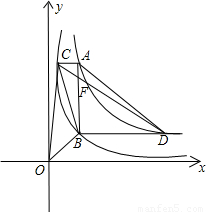
查看答案和解析>>
科目:初中数学 来源:2009年北京市西城区中考数学一模试卷(解析版) 题型:解答题
 与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.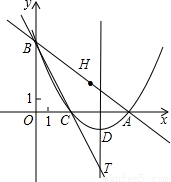
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com