
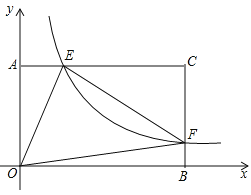
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴建立如图所示的平面直角坐标系,F是BC上的一个动点(不与B、C重合),过F点的反比例函数![]() (k>0)的图象与AC边交于点E,连接OE,OF,EF.
(k>0)的图象与AC边交于点E,连接OE,OF,EF.
(1)若tan∠BOF=![]() ,求F点的坐标;
,求F点的坐标;
(2)当点F在BC上移动时,△OEF与△ECF的面积差记为S,求当k为何值时,S有最大值,最大值是多少?
(3)是否存在这样的点F,使得△OEF为直角三角形?若存在,求出此时点F坐标;若不存在,请说明理由。
【答案】(1). F(6,![]() );(2)当k=12时,S最大为6;(3)F(6,
);(2)当k=12时,S最大为6;(3)F(6,![]() ).
).
【解析】
(1)由tan∠BOF的值求出线段BF的长度,进而得出点F的坐标;(2)设B(6,![]() ),分别表示出AE、CE、BF、CF的长度,进而表示出△OEF与△ECF的面积,最后表示出S即可;(3)分类讨论,根据相似三角形的判定与性质列方程求解即可;
),分别表示出AE、CE、BF、CF的长度,进而表示出△OEF与△ECF的面积,最后表示出S即可;(3)分类讨论,根据相似三角形的判定与性质列方程求解即可;
(1)tan∠BOF=![]() =
=![]() ,
,
∴BF=![]() ,
,
∴F(6,![]() );
);
(2)设B(6,![]() ),
),
令y=4,x=![]() ,
,
∴E(![]() ,4),
,4),
∴AE=![]() ,CE=6﹣
,CE=6﹣![]() ,BF=
,BF=![]() ,CF=4﹣
,CF=4﹣![]() ,
,
∴S△OEF=4×6﹣![]() ﹣
﹣![]() ﹣
﹣![]() ×(6﹣
×(6﹣![]() )×(4﹣
)×(4﹣![]() )=﹣
)=﹣![]() k2﹣2k+12,
k2﹣2k+12,
S△ECF=![]() ×(6﹣
×(6﹣![]() )×(4﹣
)×(4﹣![]() )=
)=![]() k2﹣k+12,
k2﹣k+12,
∴S△OEF﹣S△ECF=﹣![]() (k﹣12)2+6.
(k﹣12)2+6.
当k=12时,S最大为6;
(3)①当∠OEF=90°时,
∠AEO+∠CEF=90°,
∵∠CEF+∠CFE=90°,
∴∠AEO=∠CFE,
∵∠EAO=∠C=90°,
∴△EAO∽△FCE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得k=24或![]() ,
,
∴F(4,6)(舍去)或(6,![]() ),
),
∴F(6,![]() );
);
②当∠EFO=90°时,
同理可证△ECF∽△FBO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得k=54或24,
∴F(4,6)或(6,9),都不符合题意,
∴F(6,![]() ).
).


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
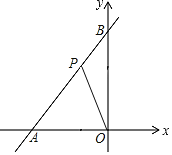
【题目】如图,一次函数y=![]() x+4与x轴、y轴分别交于点A和点B,在线段AB上有一动点P(不与点A、B重合),连接OP,当点P的坐标为_____时线段OP最短.
x+4与x轴、y轴分别交于点A和点B,在线段AB上有一动点P(不与点A、B重合),连接OP,当点P的坐标为_____时线段OP最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx经过点A(﹣1,![]() )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
)及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
(1)求抛物线的解析式;
(2)如图1,连接AO、BO,若△OAB的面积为5,求m的值;
(3)如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
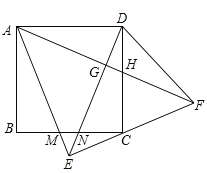
【题目】如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于点G,交CD于点H,下列结论:①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤![]() ,其中正确的有__________.
,其中正确的有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将正方形![]() 置于平面直角坐标系中,其中
置于平面直角坐标系中,其中![]() 边在
边在![]() 轴上,其余各边均与坐标轴平行.直线
轴上,其余各边均与坐标轴平行.直线![]() 沿
沿![]() 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形
轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形![]() 的边所截得的线段长为
的边所截得的线段长为![]() ,平移的时间为
,平移的时间为![]() (秒),
(秒),![]() 与
与![]() 的函数图象如图2所示,则图1中的点
的函数图象如图2所示,则图1中的点![]() 的坐标为__________,图2中
的坐标为__________,图2中![]() 的值为__________.
的值为__________.


![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.

(1)当![]() 时,
时,![]() ______________
______________![]() ;点
;点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐变____________(填“大”或“小”);
逐渐变____________(填“大”或“小”);
(2)当![]() 时,求证:
时,求证:![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状也在改变,判断当
的形状也在改变,判断当![]() 等于多少度时,
等于多少度时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△CAD与△CEB都是等边三角形,BD、EA的延长线相交于点F.
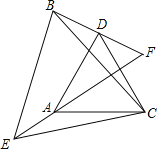
(1)求证:△ACE≌△DCB.
(2)求∠F的度数.
(3)若AD⊥BD,请直接写出线段EF与线段BD、DF之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com