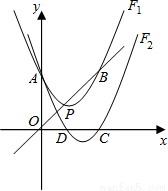
(1)解:∵F
1:y=x
2-2x+2=(x-1)
2+1,
∴P(1,1),
设直线OP的解析式为y=kx,
∴1=1×k,
即k=1,
∴直线OP的解析式为:y=x,
∵F
1的顶点坐标为P(1,1),
∴F
2的顶点坐标为(

),
∴F
2的解析式为:y=

-

,
即为:y=x
2-3x+2,
答:直线OP的解析式是y=x,抛物线F
2的函数关系式是y=

-

.
(2)解:设B(a,b),
∵直线OP:y=x与x轴的夹角是45°,
∴a=b,
∵B在抛物线y=x
2-2x+2上,
∴a=a
2-2a+2,解得:a
1=2,a
2=1(舍去),
∴B(2,2),
又∵解方程x
2-3x+2=0得:x
1=1,x
2=2,
∴D(1,0),C(2,0),
∵A(0,2),
∴OA=AB=BC=OC=2,
∵∠AOC=90°,
∴四边形OCBA为正方形,
∴OB=AC,OB⊥AC,OB与AC互相平分.
(3)解:作D点关于直线OP的对称点D′,连接D′C交OP于Q,
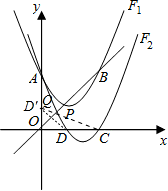
则Q为所求的点,
∵OP平分∠AOC,
∴D′的坐标是(0,1),
∴DD′=

,
设直线CD′的解析式是y=kx+1,
把C(2,0)代入得:k=-

,
∴y=-

x+1,
∵直线OP的解析式是y=x,代入得:x=-

x+1,
x=

,
即Q的坐标是(

,

),
∵D、D′关于直线OP对称,
∴DQ=D′Q,
∴DQ+CQ=D′Q+CQ=CD′=
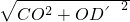
=

=

,
∴△DCQ的周长的最小值是DQ+CQ+CD=

+(2-1)=

+1.
分析:(1)化成顶点式,即可求出P的坐标,根据平移性质求出F
2的顶点坐标,即可得出抛物线的解析式;
(2)设B(a,b),得出a=b,代入y=x
2-2x+2求出B的坐标,解方程x
2-3x+2=0求出C的坐标,根据坐标得出正方形OCBA,根据正方形性质求出即可;
(3)作D关于OP的对称点D′,求出D′的坐标,连接D′C交OP于Q,则Q为所求,求出直线CD′的解析式,求出直线CD′和直线OP的交点坐标,即可得出Q的坐标,根据勾股定理求出CD′的长,即可求出三角形的周长.
点评:本题考查了轴对称-最短路线问题,正方形的性质和判定,勾股定理,解二元一次方程组,解一元二次方程,二次函数的三种形式等知识点的应用,主要考查学生综合运用这些性质进行推理和计算的能力,题目综合性比较强,有一定的难度.

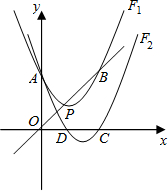 B,将抛物线F1向右平移
B,将抛物线F1向右平移 个单位,再向下平移
个单位,再向下平移 个单位得抛物线F2,抛物线F2与x轴相交于D、C两点(D在C的左边).
个单位得抛物线F2,抛物线F2与x轴相交于D、C两点(D在C的左边). ),
), -
- ,
, -
- .
.
 ,
, ,
, x+1,
x+1, x+1,
x+1, ,
, ,
, ),
), =
= =
= ,
, +(2-1)=
+(2-1)= +1.
+1.

 科学实验活动册系列答案
科学实验活动册系列答案 B,将抛物线F1向右平移
B,将抛物线F1向右平移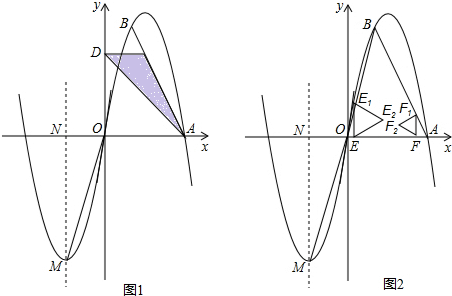
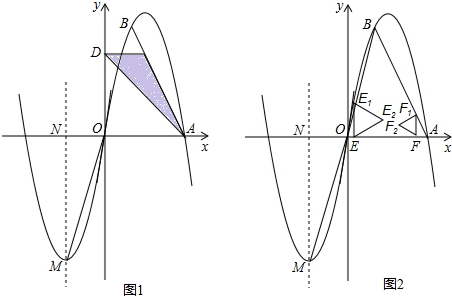
 个单位,再向下平移
个单位,再向下平移 个单位得抛物线F2,抛物线F2与x轴相交于D、C两点(D在C的左边).
个单位得抛物线F2,抛物线F2与x轴相交于D、C两点(D在C的左边).