
【题目】在平面直角坐标系![]() 中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作
中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作![]() .
.
(1)已知点![]() ,
,
①直接写出![]() 的值;
的值;
②直线![]() 与x轴交于点F,当
与x轴交于点F,当![]() 取最小值时,求k的取值范围;
取最小值时,求k的取值范围;
(2)![]() 的圆心为
的圆心为![]() ,半径为1.若
,半径为1.若![]() ,直接写出t的取值范围.
,直接写出t的取值范围.
【答案】(1)①5.②见解析;(2)![]() .
.
【解析】
(1) ①根据题意![]() 是指点
是指点![]() 到正方形
到正方形![]() 上动点
上动点![]() 的最大距离,所以当点
的最大距离,所以当点![]() 与点
与点![]() 重合时,此时
重合时,此时![]() 最大为
最大为![]() ;
;
②根据![]() 的最小值是,可知
的最小值是,可知![]() ,所以当直线
,所以当直线![]() 经过
经过![]() 和
和![]() ,即可求出
,即可求出![]() 的值;
的值;
(2)根据圆心![]() ,半径为
,半径为![]() ,可知圆
,可知圆![]() 在直线
在直线![]() 的直线上动,因为
的直线上动,因为![]() 圆上动点
圆上动点![]() 到正方形边上动点
到正方形边上动点![]() 的最大值,所以可以转化成
的最大值,所以可以转化成 ![]() 圆的半径
圆的半径![]() 圆心
圆心![]() 到正方形边上动点
到正方形边上动点![]() ,因为
,因为![]() ,可以算出
,可以算出![]() 的分界点,由于圆心
的分界点,由于圆心![]() 到点Q的最大值存在一种情况
到点Q的最大值存在一种情况![]() 时,可以计算出
时,可以计算出![]() ,刚好
,刚好![]() ,即可求出符合题意
,即可求出符合题意![]() 的取值范围.
的取值范围.
解:1.①由根据题意![]() 是指点
是指点![]() 到正方形
到正方形![]() 上动点
上动点![]() 的最大距离,所以当点
的最大距离,所以当点![]() 与点
与点![]() 重合时,此时
重合时,此时![]() 最大,即
最大,即![]()
②如图所示:
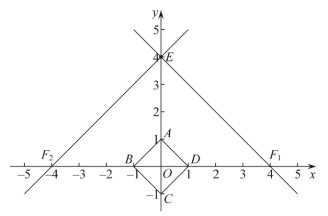
∵![]() .
.
当点![]() 的横坐标在
的横坐标在![]() 时,
时,![]() ,
,
当点![]() 的横坐标在
的横坐标在![]() 时,
时,![]() ,
,
∵![]() 要取最小值,
要取最小值,
∴![]()
∴符合题意的点F满足![]()
∴当直线![]() 经过点
经过点![]() 的坐标为
的坐标为![]() 和点
和点![]() 的坐标为
的坐标为![]() 是分别求得
是分别求得![]() .
.
∴![]() 或
或![]() .
.
结合函数图象可得![]() 或
或![]() .
.
(2)由题意可知:![]()
![]()
![]() 时
时
![]() 可计算当
可计算当![]() 时,
时,
当圆心![]() 在
在![]() 轴左侧时
轴左侧时
![]() 可以考虑到当
可以考虑到当![]() 时,
时,
利用两点之间的距离公式:
即![]()
求得:![]() ,
,
![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]()
当圆心![]() 在
在![]() 轴右侧时
轴右侧时
![]() 可以考虑到当
可以考虑到当![]() 时,
时,
利用两点之间的距离公式:
即![]()
求得:![]() ,
,
![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]()
![]()
![]()
![]()
![]()


科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
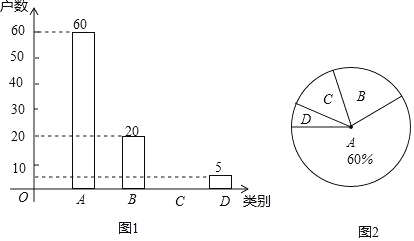
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是 ;
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.

(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率________.
②黑色方块所构拼图是中心对称图形的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况;举了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绒(![]() 为整数,总分100分),绘制了如下尚不完整的统计图表.
为整数,总分100分),绘制了如下尚不完整的统计图表.
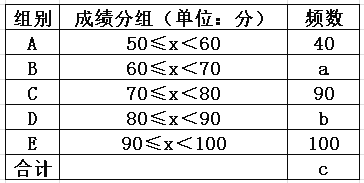

根据以上信息解答下列问题:
(1)统计表中![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)扇形统计图中,![]() 的值为________,“
的值为________,“![]() ”所对应的圆心角的度数是________(度);
”所对应的圆心角的度数是________(度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
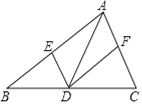
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
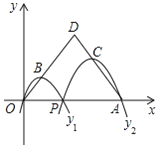
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
A.![]() B.
B.![]() C.3 D.4
C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com