
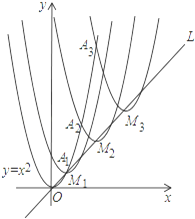
【题目】如图,抛物线y=x2在第一象限内经过的整数点(横坐标,纵坐标都为整数的点)依次为A1,A2,A3,…An,…,将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;
②抛物线依次经过点A1,A2,A3…An,….
则M2016顶点的坐标为________.
【答案】(4031,4031)
【解析】
根据抛物线的解析式,结合整数点的定义,找出点![]() 的坐标为
的坐标为![]() ,设点
,设点![]() 的坐标为(a,a),则以点
的坐标为(a,a),则以点![]() 为顶点的抛物线的解析式为
为顶点的抛物线的解析式为![]() ,由点
,由点![]() 的坐标可求出a值,可发现规律,根据规律可求出答案.
的坐标可求出a值,可发现规律,根据规律可求出答案.
解:M1(a1,a1)是抛物线y1=(x﹣a1)2+a1的顶点,
抛物线y=x2与抛物线y1=(x﹣a1)2+a1相交于A1,
得x2=(x﹣a1)2+a1,
即2a1x=a12+a1,
x=![]() (a1+1).
(a1+1).
∵x为整数点,
∴a1=1,
M1(1,1);
M2(a2,a2)是抛物线y2=(x﹣a2)2+a2=x2﹣2a2x+a22+a2顶点,
抛物线y=x2与y2相交于A2,
x2=x2﹣2a2x+a22+a2,
∴2a2x=a22+a2,
x=![]() (a2+1).
(a2+1).
∵x为整数点,
∴a2=3,
M2(3,3),
M3(a3,a3)是抛物线y2=(x﹣a3)2+a3=x2﹣2a3x+a32+a3顶点,
抛物线y=x2与y3相交于A3,
x2=x2﹣2a3x+a32+a3,
∴2a3x=a32+a3,
x=![]() (a3+1).
(a3+1).
∵x为整数点,
∴a3=5,M3(5,5),
∴点M2016的坐标为:2016×2﹣1=4031,
∴M2016(4031,4031),
故答案是:(4031,4031).


科目:初中数学 来源: 题型:
【题目】把抛物线![]() 先向左平移
先向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,得到抛物线
个单位长度,得到抛物线![]() .
.
(1)试确定![]() 的值;
的值;
(2)作原抛物线关于![]() 轴对称的图形,求所得抛物线的函数表达式.
轴对称的图形,求所得抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译![]() 若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是
若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对全市创文工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
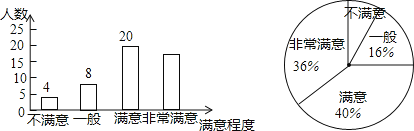
请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 分别与x轴、y轴相交与点M、N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交与点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )
分别与x轴、y轴相交与点M、N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交与点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 过点
过点![]() ,
,![]() ,过定点
,过定点![]() 的直线
的直线![]() :
:![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
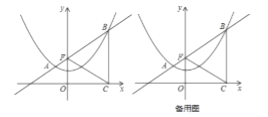
(1)求抛物线的解析式;
(2)当点![]() 在抛物线上运动时,判断线段
在抛物线上运动时,判断线段![]() 与
与![]() 的数量关系(
的数量关系(![]() 、
、![]() 、
、![]() ),并证明你的判断;
),并证明你的判断;
(3)![]() 为
为![]() 轴上一点,以
轴上一点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,设点
为顶点的四边形是菱形,设点![]() ,求自然数
,求自然数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且弧DE=弧BE.
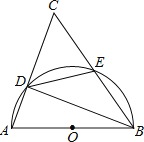
(1)试判断△ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=70°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'=______°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com