
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=![]() (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
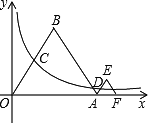
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.
|
分析:(1)过点C作CG⊥OA于点G,根据等边三角形的性质求出OG、CG的长度,从而得到点C的坐标,再利用待定系数法求反比例函数解析式列式计算即可得解; (2)过点D作DH⊥AF于点H,设AH=a,根据等边三角形的性质表示出DH的长度,然后表示出点D的坐标,再把点D的坐标代入反比例函数解析式,解方程得到a的值,从而得解. 解答:解:(1)过点C作CG⊥OA于点G, ∵点C是等边△OAB的边OB的中点, ∴OC=2,∠AOB=60°, ∴OG=1,CG= ∴点C的坐标是(1, 由 ∴该双曲线所表示的函数解析式为y= (2)过点D作DH⊥AF于点H,设AH=a,则DH= ∴点D的坐标为(4+a, ∵点D是双曲线y= 由xy= 即:a2+4a-1=0, 解得:a1= ∴AD=2AH=2 ∴等边△AEF的边长是2AD=4
点评:本题是对反比例函数的综合考查,包括待定系数法求反比例函数解析式,等边三角形的性质,解一元二次方程,难度不大,作出辅助线,表示出点C、D的坐标是解题的关键. |
|
反比例函数综合题. |


科目:初中数学 来源: 题型:
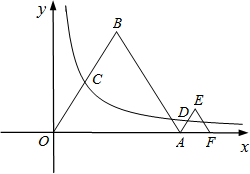 (2012•丽水)如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
(2012•丽水)如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省杭州市萧山区瓜沥一中九年级(上)月考数学试卷(10月份)(解析版) 题型:解答题
 如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙教版九年级(上)第一次月考数学试卷(六)(解析版) 题型:解答题
 如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.查看答案和解析>>
科目:初中数学 来源:2013年四川省泸州市蓝田中学中考数学模拟试卷(一)(解析版) 题型:解答题
 如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com