
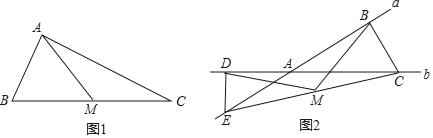
【题目】(1)如图1,在△ABC中,点M为BC边的中点,且MA=![]() BC,求证:∠BAC=90°.
BC,求证:∠BAC=90°.
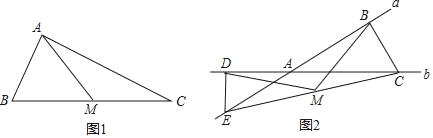
(2)如图2,直线a、b相交于点A,点C、E分别是直线b、a上两点,ED⊥b,垂足为点D,点M是EC的中点,MD=MB,DE=2,BC=3,求△ADE和△ABC的面积之比.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据点M为BC的中点,得到BM=CM=![]() BC.又MA=
BC.又MA=![]() BC,根据等量代换得到BM=CM=MA,根据等边对等角有∠BAM=∠B,∠CAM=∠C,又∠BAM+∠B+∠CAM+∠C=180°,即可得到∠BAM+∠CAM=90°,即可证明.
BC,根据等量代换得到BM=CM=MA,根据等边对等角有∠BAM=∠B,∠CAM=∠C,又∠BAM+∠B+∠CAM+∠C=180°,即可得到∠BAM+∠CAM=90°,即可证明.
(2)根据(1)的结论,可得∠EBC=90°,即可证明△ADE∽△ABC,根据相似三角形的性质即可解答.
(1)证明:∵点M为BC的中点,
∴BM=CM=![]() BC.
BC.
∵MA=![]() BC,
BC,
∴BM=CM=MA,
∴∠BAM=∠B,∠CAM=∠C,
∴∠BAM+∠B+∠CAM+∠C=180°,
∴2∠BAM+2∠CAM=180°,
∴∠BAM+∠CAM=90°,即∠BAC=90°.
(2)解:∵点M为EC的中点,ED⊥AC于点D,
∴DM=![]() EC.
EC.
∵BM=DM,
∴BM=![]() EC,
EC,
∴∠EBC=90°.
∴∠ADE=∠ABC=90°.
又∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
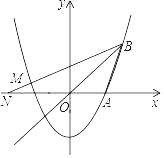
【题目】如图,抛物线y=![]() x2+bx+c过点A(2,0)和B(3,3).
x2+bx+c过点A(2,0)和B(3,3).
(1)求抛物线的表达式;
(2)点M在第二象限的抛物线上,且∠MBO=∠ABO.
①直线BM交x轴于点N,求线段ON的长;
②延长BO交抛物线于点C,点P是平面内一点,连接PC、OP,当△POC∽△MOB时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
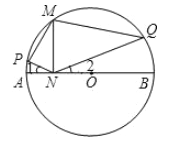
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 上一点,
上一点,![]() ,垂足为
,垂足为![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上一点(不与端点重合),如果
上一点(不与端点重合),如果![]() ,下面结论:①
,下面结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是( )
.其中正确的是( )
A. ①②③B. ①③⑤C. ④⑤D. ①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径CD为2,弧AC的度数为80°,点B是弧AC的中点,点P在直径CD上移动,则BP+AP的最小值为( )
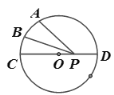
A. 1B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设m,n是任意两个实数,规定m,n两数较大的的数称作这两个数的“绝对最值”,用sec(m,n)表示。例如:sec(-1,-2)=-1,sec(1,2)=2,sec(0,0)=0,参照上面的材料,解答下列问题:
(1)sec(![]() ,3.14)=________,sec(
,3.14)=________,sec(![]() ,
,![]() )=__________;
)=__________;
(2)若sec(-3x-1,x+1)=-3x-1,求x的取值范围;
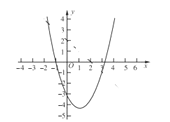
(3)求函数![]() 与
与![]() 的图象的交点坐标,函数
的图象的交点坐标,函数![]() 图象如图所示,请你在图中作出函数
图象如图所示,请你在图中作出函数![]() 的图象,并根据图象直接写出sec(-x+2,
的图象,并根据图象直接写出sec(-x+2, ![]() )的最小值。
)的最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
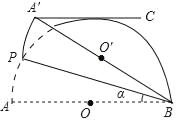
【题目】如图,AB是半圆O的直径,点P(不与点A,B重合)为半圆上一点,将图形沿BP折叠,分别得到点A,O的对应点点A′,O′,过点A′C∥AB,若A′C与半圆O恰好相切,则∠ABP的大小为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
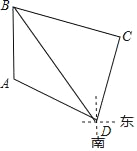
【题目】分别静止在A、B处(B在A的正北方)是我国两艘军舰相距10km,为在D处的一艘我国货轮执行护航任务,A处军舰测得D点在南偏东63.4°,B处军舰测得D点在南偏东36.8°.货轮沿着北偏东16.4°方向航行了12km到达C点,此时在B处的军舰测得C点在南偏东73.6°方向上.
(1)求∠BCD的度数;
(2)求AD的长.(参考数据:sin36.8°≈0.60,cos36.8°≈0.80,tan26.6°≈0.50,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
(1)求证:直线EF是⊙O的切线;
(2)若CF=3,cosA=0.4,求出⊙O的半径和BE的长;
(3)连接CG,在(2)的条件下,求CG:EF的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com